Influence of freestream Reynolds number

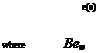It’s useful to examine the effect of freestream Reynolds number on the transition location as indicated by relation (4.123). Laminar boundary layer theory indicates that the momentum thickness (or any other integral thickness) scales as 9 ~ I / /lie. For example, Thwaites method for a constant //,. = V. gives

and c is a global reference length such as the chord. Therefore, the N-factor growth rate scales as /Hr via the 1/9 factor which multiplies fTS in (4.121). In addition, the local momentum-thickness Reynolds number in this case is

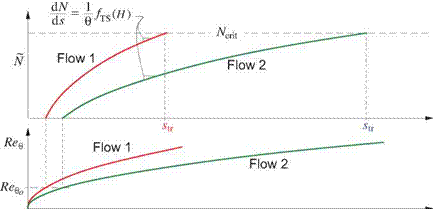
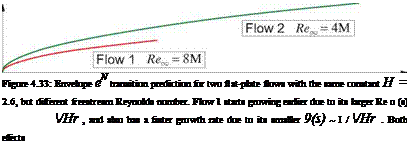
which affects where the growth begins via the Be$o(H) threshold function. The effects are illustrated in Figure 4.33 for two Blasius flows with different freestream Reynolds numbers. As Reincreases, N(s) starts growing sooner because the larger Re о reaches Re oo (2.6) sooner, and also grows faster because of the smaller 9(s). Both effects contribute to moving transition upstream with increasing Re.

s