LATERAL STABILITY CHARACTERISTICS OF AIRPLANES

Lateral stability is a function of the yawing and rolling moments, the lateral force and their associated cross coup­ling. The stability of the airplane from these forces and moments must be determined by a dynamic analysis as the motion is time dependent. However, the most impor­tant contribution to such a dynamic stability analysis comes from so-called “static” stability derivatives, i. e. from the derivatives of forces and moments with angles of roll, yaw and pitch. Static stability is, therefore, consid­ered first while principles, derivatives, theory and practical results of dynamic lateral stability are presented in the last part of this chapter.

Static Stability. Evaluation of theoretical and experimen­tal derivatives of wings as a function of the angle of yaw is broken down into:

(a) characteristics of straight wings

(b) derivatives of dihedraled wings

(c) analysis of swept wings.

Under each of these headings we will consider the varia­tion of lateral forces, the rolling moment (about the longitudinal axis) and yawing moments (about the vertical or normal axis).

Components. When rotating an airplane about the two axes considered in this chapter, the three basic parts — wing, fuselage (also engine nacelles if any) and vertical tail surface — each contributes components of aerodynamic forces and/or moments. We will consider these compo­nents separately:

(aa) characteristics of the wing as listed above (bb) moments and/or influence of the “fuselage”

(cc) forces and moments due to the vertical tail.

We will also have to include mutual interactions between those airplane parts. In fact, the fuselage usually does not contribute any rolling moment of its own, however, it may change those moments of the wing.

Nomenclature. Besides the basic symbols listed in t ie first chapter, we will specifically use the following in the treatment of lateral characteristics:

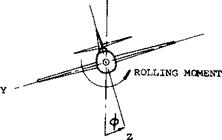
Y = lateral force “L” = rolling moment N = yawing moment.

The symbol “L” (from “longitudinal”, indicating the axis about which the moment is defined) should not be con­fused with L, denoting lift. Lateral characteristics are presented in the form of non-dimensional coefficients:

Cy = Y/qS; C* = “L”/qSb; Cn = N/qSb (1)

Note that the moments are referred to the span (and not to the half span as found in some of the sources referred to). In the discussion of lateral characteristics, the follow­ing terms should also be understood:

1) “Yaw” indicates an angular displacement (by the angle jB) about the normal axis x axis of the airframe.

2) “Yawing” indicates an angular rate of motion about the same axis.

3) “Sideslipping” indicates a lateral velocity in the direc­tion of the wing span.

Derivative Notation. The notation developed in dealing with the equations of motion and the analysis of aircraft stability greatly simplifies the task and helps in the overall understanding. This system is generally used in the indus­try and the research agency and is adopted for this chap­ter. The important derivatives used are per radian unless otherwise noted and are:

Сі* = д C*/<3/9

Effective dihedral, rate of change of rolling moment coefficient with angle of sideslip.

Є os ~ ^ C„/ dB

Directional-stability derivative, rate of change of yaw­ing-moment coefficient with angle of sideslip.

Cy/> — d Су /dp

Lateral-force derivative, rate of change of lateral-force coefficient with angle of sideslip.

C„T =d Ch/*(rb/2V)

Damping-in-yaw derivative, rate of change of yawing – moment coefficient with yawing-angular-velocity fac­tor.

cnp = c„/a(pb/2V)

Rate of change of yawing-moment coefficient with rolling-angular-velocity factor.

C/p =Q4(pb/2V)

Damping-in-roll derivative, rate of change of rolling – moment coefficient with rolling-angular-velocitv fac­tor.

Qr =d Q/4(rb/2V)

Rate of change of rolling-moment coefficient with yawing-angular-velocity factor.

CyP =6 Су U(pb/2V)

Rate of change of lateral-force coefficient with rolling-angular-velocity factor.

СуГ = & Су 16 (rb/2V)

Rate of change of lateral-force coefficient with yawing-angular-velocity factor.

Systems of Reference. The rolling moment is basically taken about the longitudinal axis of the airplane (air­frame); and the yawing moment is about the axis normal to both the longitudinal axis and the wing span. This system of reference which we may call the airframe system is the one in which a pilot senses position and motion of his airplane. There is also the “wind system”, however; as we may have it, for example, in such wind tunnels where the balance is fixed to the tunnel, while the wing or airplane model is rotated in reference to the balance to produce the angle of yaw. As far as rolling is concerned, the difference between the moment measured about the longitudinal airplane axis and that about the direction of flow or flight is usually very small; it corre­sponds to the cosine of the angle of yaw (1). Accordingly, when considering derivatives taken at small angles of at­tack and about the neutral position (at^ = zero), there is no difference between the two systems as far as moments are concerned. As we will see later, considerable differ­ences can arise, however, in the lateral force Y depending on the direction, either along the wing span or normal to the direction of flow or flight in which it is measured or defined.

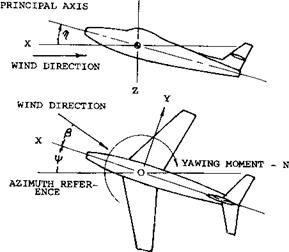
Stability Axis. The axis system most universally used is stability axis, figure 1, and is used in this chapter unless otherwise stated. In this system the Z-axis is in the plane of symmetry and perpendicular to the relative wind, the X-axis is in the plane of symmetry of the airplane and is perpendicular to the Z-axis, and the Y-axis is perpendicu­lar to the plane of symmetry. The sign convention used with the stability axis is shown on figure 1. In this sign convention: [124]

Figure 1. Stability axis system, positive direction indicated for forces, moments and displacement.

a) The rolling moment derivative dQ/d^ is considered to be negative when the advancing wing tip (or wing panel) is lifted by the moment.

b) The derivative of the yawing moment is defined as positive when the moment tends to return the airplane to the neutral,^ = 0 position.

c) The lateral force derivative is defined as positive when the force causes the airplane to move to the right.