Longitudinal dihedral

The tail plane is usually set at an angle less than that of the main planes, the angle between the chord of the tail plane and the chord of the main planes being known as the longitudinal dihedral (Fig. 9.3). This longitudinal dihedral is a practical characteristic of most types of aeroplane, but so many considerations enter into the problem that it cannot be said that an aeroplane which does not possess this feature is necessarily unstable longitudinally. In any case, it is the actual angle at which the tail plane strikes the airflow, which matters; therefore we must not forget the downwash from the main planes. This downwash, if the tail plane is in the stream, will cause the actual angle of attack to be less than the angle at which the tail plane is set (Fig. 5.6). For this reason, even if the tail plane is set at the same angle as the main planes, there will in effect be a longitudinal dihedral angle, and this may help the aeroplane to be longitudinally stable.

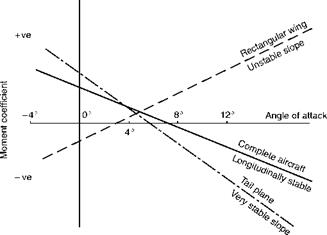
Fig 9.2 Pitching moment coefficient about centre of gravity Wing, tail plane and complete aircraft.

Fig 9.3 Longitudinal dihedral angle

Suppose an aeroplane to be flying so that the angle of attack of the main planes is 4° and the angle of attack of the tail plane is 2°; a sudden gust causes the nose to rise, inclining the longitudinal axis of the aeroplane by 1°. What will happen? The momentum of the aeroplane will cause it temporarily to con­tinue moving practically in its original direction and at its previous speed. Therefore the angle of attack of the main planes will become nearly 5° and of the tail plane nearly 3°. The pitching moment (about the centre of gravity) of the main planes will probably have a nose-up, i. e. unstable tendency, but that of the tail plane, with its long leverage about the centre of gravity, will defi­nitely have a nose-down tendency. If the restoring moment caused by the tail plane is greater than the upsetting moment caused by the main planes, and possibly the fuselage, then the aircraft will be stable.

This puts the whole thing in a nutshell, but unfortunately it is not quite so easy to analyse the practical characteristics which will bring about such a state of affairs; however the forward position of the centre of gravity and the area and leverage of the tail plane will probably have the greatest influence.

It is interesting to note that a tail plane plays much the same part, though more effectively, in providing longitudinal stability, as does reflex curvature on a wing, or sweepback with wash-out of incidence towards the tips.

When the tail plane is in front of the main planes (Fig. 5E) there will prob­ably still be a longitudinal dihedral, which means that this front surface must have greater angle than the main planes. The latter will naturally still be at an efficient angle, such as 4°, so that the front surface may be at, say, 6° or 8°. Thus it is working at a very inefficient angle and will stall some few degrees sooner than the main planes. This fact is claimed by the enthusiasts for this type of design as its main advantage, since the stalling of the front surface will prevent the nose being raised any farther, and therefore the main planes will never reach the stalling angle.

In the tail-less type, in which there is no separate surface either in front or behind, the wings must be heavily swept back, and there is a ‘wash-out’ or decrease in the angle of incidence as the wing tip is approached, so that these wing tips do, in effect, act in exactly the same way as the ordinary tail plane (Figs 5C and 5D).