Pressure and Force Information

The perturbation velocity field for the flow at angle of attack past a slender body of revolution is obtained by adding the results from Sections 8.3.1 and

8.3.2. The velocity field will be evaluated on the body surface for the determination of the forces and pitching moment.

For the axisymmetric problem of Section 8.3.1, the radial velocity component is given by the boundary condition (Eq. (8.108a)) as

qr = Q-R'(x) (8.127)

The axial component of velocity can be determined by taking the limit of Eq.

(8.117) as the radial coordinate approaches zero. Let us denote this component as

4x = Qxa (8.128)

It is given in Karamcheti15 (p. 577) as

qxA = 2^S”(x)ln^ + 4^ (s"'(x0)lnx-x0dx0 (8.128a)

The radial, tangential, and axial velocity components of the transverse problem of Section 8.3.2 are found by substituting r = R in Eqs. (8.124-8.126). The complete velocity distribution on the body surface is obtained by adding the free-stream components from Eq. (8.106) to the perturbation components to get

q(x, г, в) = (6« + qx, Q^a sin в + qr, Q^a cos в + qe) (8.129)

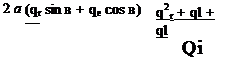Substituting Eq. (8.129) into the pressure coefficient equation yields

It can be seen by an inspection of the velocity components that the magnitude of the squares of the crossflow plane components is comparable to the magnitude of the axial component itself and therefore the only term in the pressure coefficient equation that can be neglected is ql/Qi. The perturbation components from Eqs. (8.124-8.126) are substituted into the modified Eq. (8.130) and after some manipulation the pressure coefficient becomes

Cp = ~ (R’)2 ~ 4aR’ sin в + 0^(1 — 4 cos2 в) (8.131)

и*~(Т Js Jo Jo

The force acting on the slender body is given by

where dx is the slender-body approximation for the length element. The slender-body approximation for the unit normal is

n = er – R ‘e, = — R ‘ex + cos 6ey + sin 6ez (8.133)

and substituting this into Eq. (8.133) yields the force components in the three coordinate directions:

Fx = f f R’RpdQdx Jo Jo	(8.134a)
ГІ ґ2 71 Fy = – Rp cos OdOdx Jo Jo	(8.1346)
Fz = — [ [ Rp sin в d6 dx Jo Jo	(8.134c)
The rate of change of the force components with respect	to x is given by
dFx С2л – r=-RR pde dx J0	(8.135a)
dF f2jT -r2 = —R p cos в d6 dx J0	(8.1356)
dFz С2л —— – – R psinddd dx J0	(8.135c)
To use the pressure coefficient from Eq. (8.131) in Eqs. (8.135) the pressure is written as
P = kpQlCp + Pa,	(8.136)

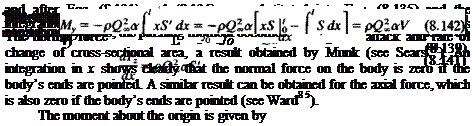where V is the body volume

8.3.1 Conclusions from Slender Body Theory

The above results for the aerodynamic forces acting on slender bodies show that for pointed bodies there is no lift and no drag force, but there is an
aerodynamic pitching moment. This important result is very useful when checking the accuracy of numerical methods that calculate the lift and drag by integrating the surface pressure over the body (and may result in lift and drag that are different from zero). Lift and drag forces are possible only when the base is not pointed, and a base pressure exists that is different from that predicted by potential flow theory (e. g., due to flow separations). Some methods for the treatment of bodies with blunt bases are presented by Nielsen.8,6