Time Response

8.1. Time Response

of Conventional Pressure Sensitive Paint

8.1.1. Solutions of Diffusion Equation

The fast time response of PSP is required for measurements in unsteady flows, which is related to two characteristic timescales of PSP. One is the luminescent lifetime of PSP that represents an intrinsic physical limit for an achievable temporal resolution of PSP. Another is the timescale of oxygen diffusion across a PSP layer. Because the timescale of oxygen diffusion across a homogenous polymer layer is usually much larger than the luminescent lifetime, the time response of PSP is mainly determined by oxygen diffusion. In a thin homogenous polymer layer, when diffusion is Fickian, the oxygen concentration [O2] can be described by the one-dimension diffusion equation

where Dm is the diffusivity of oxygen mass transfer, t is time, and z is the coordinate directing from the wall to the polymer layer. The boundary conditions at the solid wall and the air-paint interface for Eq. (8.1) are d[O2]/d z = 0 at z = 0,

[O2] = [O2 ]o f (t) at z = h, (8.2)

where the non-dimensional function f( t) describes a temporal change of the oxygen concentration at the air-paint interface, [O2 ]0 is a constant concentration of oxygen, and h is the paint layer thickness. The initial condition for Eq. (8.1) is [O2] = [O2]0f(0) att = 0. (8.3)

Introducing the non-dimensional variables

n(t’ ,z’) = [O2]/[O2]0 – f(0), z’ = z/h, t’ = tDm/h2, (8.4)

we have the non-dimensional diffusion equation

dn _ d2n

dt ~d^

with the boundary and initial conditions

dn/dZ_ 0 at z _ 0 , n _ g(t’) at z’_ 1, n _ 0 at t _ 0 , (8.6)

where the function g( t’) is defined as g(t’) _ f(t’)- f(0) that satisfies the initial condition g(0) _ 0 .

Applying the Laplace transform to Eq. (8.5) and the boundary and initial conditions Eq. (8.6), we obtain a general convolution-type solution for the normalized oxygen concentration n(t’ ,z’)

In Eq. (8.7), the function gt(t) _ dg(t)/dt _ df(t)/dt is the differentiation of g(t) with respect to t and the function W(t, z) is defined as

W(t, z) _ V (-1)kerfc(1 + 22k z ) + У (-1)keifc(1^). k_0 Mt k_0 2jt

The derivation of Eq. (8.7) uses the following expansion in negative exponentials [1 + exp( -2л[1)]- ^ (-1 )n exp( -2^[s ), where s is the complex variable of

n_0

the Laplace transform. In particular, for a step change of the oxygen concentration at the air-paint interface, after gt(t) _ S(t) is substituted into Eq. (8.7), the oxygen concentration distribution in a paint layer is simply n(t’,z ) _ W(t’,z’), a classical solution given by Crank (1995) and Carslaw and Jaeger (2000).

Instead of using the Laplace transform, Winslow et al. (2001) studied the solution of the diffusion equation using an approach of linear system dynamics. The special solutions for a step change and a sinusoidal change of oxygen were used for PSP dynamical analysis by a number of researchers (Winslow et al. 1996, 2001; Carroll et al. 1995, 1996; Mosharov et al. 1997; Fonov et al. 1998). The trigonometrical-series-type solution for a step change of oxygen given by Carroll et al. (1996) is

where Ak _ -2( -1 )k /(hXk), Xk _ (2k -1 )n/( 2h), [O2 ]max _ [O2 ](t, h), and [O2 ]min _ [O2 ](0,z). Similarly, Winslow et al. (1996) used the trigonometrical – series-type solution for a sinusoidal change of oxygen

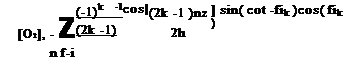[O2 ](t, z)-[O2 ]o –

where

The constants [O2 ]0 and [O2 ]1 are given in the initial and boundary conditions [O2 ](0,z) – [O2 ]o and [O2 ](t, h) – [O2 ]o + [O2]1 sin(ot).

Mosharov et al. (1997) also presented the trigonometrical-series-type solution of the diffusion equation in a similar form to Eq. (8.9) for a step change at a surface. Note that they defined a coordinate system in such a way that the air- paint interface was at z – 0 and the wall was at z – h. For a sinusoidal change of oxygen [O2 ](t,0) – [O2 ]0 + [O2 ]1 sin( ot) at the air-paint interface, they gave a solution composed of two harmonic terms, i. e.,

[O2](t, z) – [O2]0 + [O2]1[ X(y, z’ )sin( ot) + Y(y, z’ )cos( ot)] , (8.11)

where у-(oh2 /Dm)1/2 is a non-dimensional frequency and z!- z/h is a non­dimensional coordinate normal to the wall. The coefficients in Eq. (8.11) are X(Y, z’)-

cosh[42 y(1 – z! /2)] cos( у z! / 42)+cos[42 y(1 – z! /2)] cosh( у z! / 42)
cos h(j2 y)+ cos Ы2 y)

Y( Y, z! ) –

sinh[-[2 y( 1 – z!/ 2)] sin( yz! / V2 )+sin[j2 y(1 – z! / 2)] sinh( yz!/y[2 ) .
cos h(42 y)+ cos Ф y)

(8.12)

These trigonometrical-series-type solutions, which are often obtained using the method of separation of variables, should be equivalent to the general convolution-type solution Eq. (8.7) that is reduced in these special cases.

The solutions of the diffusion equation give a classical square-law estimate for the diffusion timescale Tdiff through a homogenous PSP layer,

rdiff ~ h2/Dm. (8.13)

The square-law estimate is actually a phenomenological manifestation of the statistical theory of the Brownian motion. Interestingly, this estimate is still valid even when the diffusivity of a homogeneous polymer is concentration-dependent. The 1D diffusion equation with the concentration-dependent diffusivity can be
reduced to an ordinary differential equation by using the Boltzmann’s transformation % = z/(2t1/2); hence, the solution for the concentration distribution can be expressed by this similarity variable (Crank 1995). Clearly, the Boltzmann’s scaling indicates that the timescale for any point to reach a given concentration is proportional to the square of the distance (or thickness).

Using the solution of the diffusion equation for a step change of pressure, Carroll et al. (1997) estimated the mass diffusivity Dm for oxygen in a typical

silicon polymer binder and gave Dm = 1.23-1.88x 10- m2/s over a temperature range of 9.9-40.2oC. The values of Dm = 3.55x 10- m2/s for the pure polymer Poly(dimethyl Siloxane) (PDMS) and Dm = 1.2x 10-9 m2/s for PDMS with 10% fillers were also reported (Cox and Dunn 1986; Pualy 1989). For a 10 |jm thick polymer layer having the diffusivity Dm = 10~10 -10- m2/s, the diffusion

timescale is in the order of 0.1-1 s. Therefore, a conventional non-porous polymer PSP has slow time response, and it is not suitable to unsteady pressure measurements.