Torsional Damping

As mentioned previously, the highly nonlinear airloads obtained by operating the rotor in proximity to retreating blade stall can introduce aeroeiastic stability problems. One problem is called stall flutter, and this occurs when negative aerodynamic damping changes an otherwise stable aeroeiastic blade mode into a divergent or high amplitude limit cycle oscillation. The problem is particularly important for the torsion mode. A torsional damping factor, D. F. or Cw can be defined by the line integral

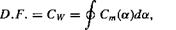(9.1)

which is positive when it corresponds to a counterclockwise loop in the Cm versus a curve – see Carta (1967). If the torsional damping is negative, this would tend to promote an aeroeiastic divergence or flutter situation.

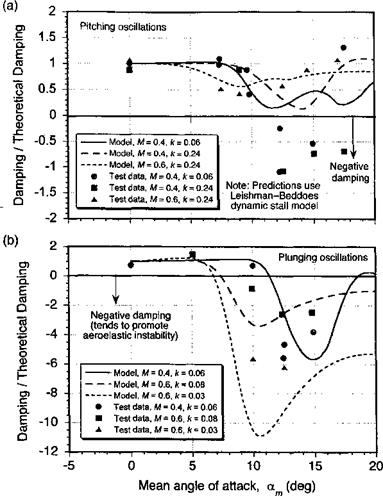
The progressive change from positive to reduced or negative torsional damping (for a given amplitude and reduced frequency of oscillation) is apparent as the mean AoA is increased into dynamic stall, as previously illustrated by the results shown in Fig. 9.4. It has been shown that the onset of light dynamic stall introduces a second clockwise loop of negative damping so that the pitching moment curve now looks like a figure eight. This second loop then grows in size with increasing mean AoA. Further penetration into dynamic stall produces a moment break that is now early enough in the oscillation cycle that the peak nose-down moment occurs while the AoA is still increasing. This introduces another new loop in the counterclockwise (positive) sense. More positive torsional damping is recovered when deep stall penetration occurs. Increasing the reduced frequency can act to delay the onset of stall to a higher AoA and can suppress the amount of flow separation, thereby reducing the negative damping, as shown previously by means of Fig. 9.5.

The aerodynamic torsional damping of an airfoil in the dynamic stall regime is a very difficult quantity to predict. While the various semi-empirical dynamic stall models appear

to give good predictions of the net forces and pitching moments, they do not always give good estimates of torsional aerodynamic damping. Because damping is an integrated quan­tity, the combination of conditions that determine dynamic stall onset and phasing of the center of pressure movement during vortex shedding must be determined very accurately. Measurements of the overall torsional damping trend versus mean AoA, am, is shown in Fig. 9.10, for both pitch and plunge forcing. Predictions were made using the Leishman – Beddoes dynamic stall model. The damping is normalized by the theoretical damping as given by the classical incompressible flow unsteady aerodynamic theory. Using the results in Chapter 8, then for pitching oscillations

Cm = 2^2 (nVba + ^k Qfc – i) aelcot = Cm sin (cot + ф), (9.2)

where

Cm – 1 + ^k2 and Ф = sin 1 ) .

Substituting this expression into Eq. 9.1 gives

Cw — TtkaJ 1 4—— k2,

64

where aeq is the equivalent AoA (as defined in Eq. 8.182). By a similar process, the theo­retical torsional damping for plunging motion is found to be

The results in Fig. 9.10 show that in fully attached flow the torsional damping for an airfoil undergoing pitching motion is approximately twice that for equivalent plunging motion. This is because of the effects of pitch rate contributions to the noncirculatory pitching moment, which causes the area contained within the moment loop to be greater for a pitching airfoil than for a plunging airfoil under the same equivalent time-history of AoA forcing. This result is also seen in the experimental measurements (see Figs. 8.32 and 8.33).

The explanation for the observed behavior of the torsional damping can be deduced from Figure 9.4, where it has been shown that for higher mean AoA the pitching moment develops into two loops at dynamic stall onset, with a decrease in torsional damping. With further increase in mean AoA, the second loop increases in size and the net damping during the cycle rapidly decreases. Figure 9.10 shows that for both the pitch and plunge cases very low or negative damping is obtained at dynamic stall onset. At some point, just after stall onset, the mean AoA is sufficient such that significant negative damping reoccurs for the plunge oscillation. Although stall onset occurs at a lower equivalent AoA for an airfoil oscillating in pitch, the inherently lower damping for the plunging airfoil in attached flow means that the damping may well become negative at a lower mean AoA for conditions of oscillatory plunging. As the mean AoA is increased further, the damping increases again and ultimately becomes positive when fully separated flow conditions exist. See Carta (1967) for a detailed discussion of torsional damping under dynamic stall conditions.