TS-wave natural transition prediction

Many types of exponentially-growing instabilities can precipitate natural transition. The most common types in 2D-like flows are called Tollmien-Schlichting (TS) waves, which are sinusoidally-oscillating pressure and velocity perturbations within the boundary layer (see Schlichting [12] and Cebeci and Bradshaw [20]). The TS wave perturbations initially have very small amplitudes near the leading edge, usually orders of magni­tude smaller than ue. For unstable waves these amplitudes grow exponentially downstream to levels suffi­cient to trigger transition, roughly a few percent of ue. The ratio of the local to initial TS wave amplitudes is defined as eN, where the exponent N(s) is the so-called “N-factor” which quantifies the instability growth. In the “envelope eN” transition prediction method, the N-factor is computed by an accumulating integral over the upstream surface, much like the P(s) and K(s) defects are accumulated as indicated in Figure 4.8.

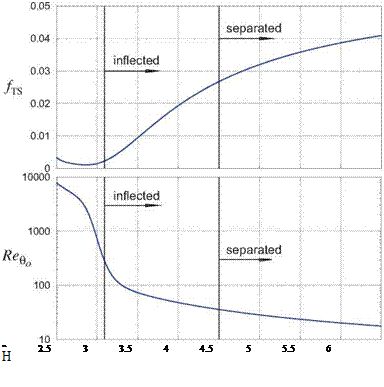
The empirical functions fTS(H) and Rego(H) which determine the IN(s) growth are shown in Figure 4.31. Curve fits are provided by Drela [6]. Transition is assumed to occur at the s location where the N(s) variable reaches a specified critical value Ncrit, which is a measure of the ambient noise or disturbance level.

1.12.4 Influence of shape parameter

For self-similar (power-law) flows, the TS growth rate functions can be used to explicitly determine the Reg value at the transition location, and also the corresponding Rex value.

( — ) = Be. gtr(H, Ncl, t) = Reg0{H) + ^—————- (4.122)

V v Ar dN/dReg (H)

(t2),, ^ = (*««.- t)2 wm)

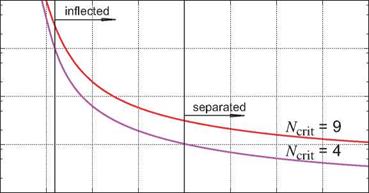
Figure 4.32 shows this Rextr versus the H value of the self-similar flow, for two typical Ncrit values. Note the dramatic sensitivity of the transition location on the shape parameter H. Between the Blasius and incipient-separation flows, H = 2.6 and 4.0, the transition distance is reduced by roughly a factor of 100.

The transition location also depends on the specified parameter Ncrit, which is a measure of the initial TS wave amplitude, or in effect the ambient disturbance level together with some degree of receptivity. Since the initial disturbances must be amplified by a factor of eNcrit to precipitate transition, a large Ncrit value corresponds to a clean flow, and vice versa. Ncrit = 11 or 12 is a typical value in a very clean flow like a sailplane in flight, Ncrit = 9 is appropriate for the flow in a very quiet wind tunnel, while Ncrit = 4 corresponds to a fairly turbulent environment such as in a noisy wind tunnel. Note that e9 ~ 8100 and e12 ~ 163 000, so enormous amplifications are required for TS waves to trigger transition in clean flows.

1e+07

10000 1000

2 2.5 3 3.5 4 4.5 5 5.5 6

H

Figure 4.32: Transition Reynolds number versus shape parameter H for self-similar flows, as pre­dicted by the envelope eN method for two Ncrjt values. Transition Reynolds number for incipient- separation flow (H = 4.0) is about 100 times smaller than for Blasius flow (H = 2.6).