Wake Potential Jump

The idealized far-field force components will be seen to depend on the potential jump Ap(s) across the ideal­ized wake sheet in the far-downstream Trefftzplane. The objective here is to relate Ap(s) to the aerodynamic parameters of the lifting body which generated the sheet.

A thin wake layer must have a zero static pressure jump Ap = pi — pu across it. Assuming the total pressure is the same on the upper and lower sides of the wake vortex sheet, the compressible or incompressible steady Bernoulli equation then implies a zero jump in the velocity magnitude. We then have,

0 0 0

0 (5.15)

V0 = i(V„+V/)

AV = Vu—Vi

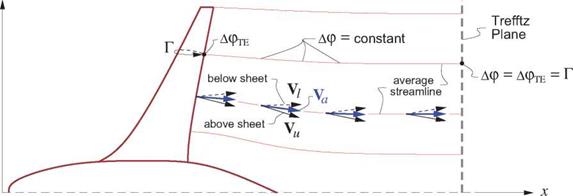
where V denotes the average sheet velocity, shown in Figure 5.5. In the final relation (5.15), the velocity jump AV was replaced by the equivalent surface gradient of the potential jump Ap.

Equation (5.15) states that the gradient of the sheet potential jump Ap(s, e) is perpendicular to Va, or equiv­alently that Ap(s, e) is constant along the average sheet streamlines which are everywhere parallel to Va, as shown in Figure 5.5. Hence, the ApTE value at the body’s trailing edge where the sheet is shed persists downstream along the average streamline into the Trefftz plane. This ApTE is also the circulation Г about a contour around the wing or body section which contains that trailing edge point.

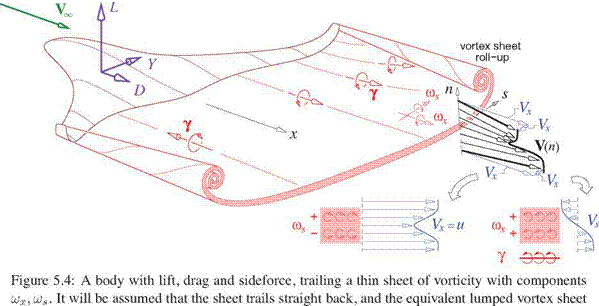
In principle one could trace the average wake streamlines from the wing trailing edge to determine its shape y(s),z(s) and loading Ap(s) in the far-downstream Trefftz plane. This would require tracking the roll-up process in detail which for most cases is impractical. A more common and much simpler approach is to trace the wake streamlines straight back along the freestream direction. This is equivalent to assuming

Va ~ Vo (straight-wake assumption) (5.16)

which is the model shown in Figures 5.6 and 5.7 in the following sections.