ANOVA-Analysis

With the ANOVA analysis (Analysis of Variances) the influence of each parameter and interaction on the result of the simulation is obtained. In this section a short summary of this statistical method is given. Thereby the variable y is the result of

Orthogonal Array	Number of lines	Max. No. of parameters	Max. Number of columns for given Number of levels
2	3	4	5
L4	4	3	3	–	–	–
4	8	7	7	–	–	–
*"9	9	4	–	4	–	–
l12	12	11	11	–	–	–
*-16	16	15	15	–	–	–
*- 16	16	5	–	–	5	–
*"18	18	8	1	7	–	–
*“25	25	6	–	–	–	6
*"27	27	13	–	13	–	–
*"32	32	31	31	–	–	–
*" 32	32	10	1	–	9	–
*"36	36	23	11	12	–	–
*"36	36	16	3	13	–	–
*-50	50	12	1	–	–	11
к»	54	26	1	25	–	–
*"64	64	63	63	–	–	–
*" 64	64	21	–	–	21	–
*"81	81	40	–	40	–	–

Fig. 2 Overview about pre-defined Taguchi matrices

the CFD simulation, n is the number of simulations and f is the degree of freedom. First of all the mean square error is determined by

(V V’)2

SQin = -^-h— = CF. (1)

n

The degree of freedom of the mean square values is

fsQm = n – (n – 1) (2)

In the next step the total error square sum is determined.

SQtotal = (ZV»)2 – CF. (3)

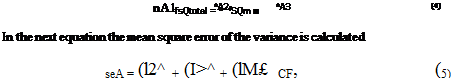
It has the degree of freedom

exemplarily shown for a parameter A with 3 levels. The results of the simulations with the same level for parameter A are summed, squared and divided by the number

of simulations with the same level of parameter A. Then the sum of the mean square values CF is subtracted. The degree of freedom is

fSQA = nLevels – fsQm, (6)

where nLevels are the number of levels of parameter A. The squared variances of the interactions are calculated by

SQm-b = і1У{АхВ)і) – CF – SQa – SQb, (7)

n(AxB)i

shown exemplarily for parameter A and B. The results of the simulations where the level combination of parameter A and B is the same are summed, squared and divided by the number of results with the same level combination. Then the sum of the mean square values and the mean square errors of parameter A and B are subtracted.

In the next step the estimation variances of each parameter are estimated by

again shown for parameter A. Then the evaluation of the critical Fi can be performed.

This value shown here for the parameter A is compared to the so called Fisher values. The Fisher value is a reference value used for the determination of the dif­ferences of variances with a certain probability of confidence. Reference values are given in so called Fisher tables depending on the probability of confidence. If the calculated Fisher value is larger than the value given by the Fisher table, the null hypothesis will be rejected. It is assumed that the differences from the total mean value are not random (null hypothesis). Therefore the alternative hypothesis is valid. If the null hypothesis is rejected, it can be assumed that an influence of the tested parameter is existent. For the percental influence of each parameter the adjusted error square sum must be determined first.

SQA = SQa – fAVF (10)

Dividing this value by the squared variances and multiplying it with 100. the per­centage influence of the parameter (here shown for parameter A) on the results of the simulation is obtained.