Concluding Remarks

In this chapter, we have offered an overview of the various low Reynolds number flyers, discussing simple mechanics for several flight modes and highlighting flight characteristics and scaling laws related to wingspan, wing area, wing loading, wing – beat frequency, and vehicle size and weight.

The scaling laws indicate that, as a flyer’s size reduces, it has to flap faster to stay in the air, experiences lower wing loading, is capable of cruising slower, has a lower stall speed, and, consequently, can survive much better in a crash landing. In addition, as a flyer becomes smaller, its weight shrinks at a much faster rate, meaning that it can carry very little “fuel” and has to resupply frequently. Birds, bats, and insects apply different flapping patterns in hovering and forward flight to generate lift and thrust. Typically, in slow forward flight the reduced frequency and wing-beat amplitude tend to be high, resulting in highly unsteady flow structures. In fast forward flight the reduced frequency and the wing-beat amplitude tend to be low, and the wake often consists of a pair of continuous undulating vortex tubes or line vortices. Larger birds have relatively simple wingtip paths in comparison to smaller flyers. We have also discussed the power requirement associated with flight, including the L-shaped curve between specific power and flight speed.

As a flyer’s size reduces, its operating Reynolds number becomes lower. As detailed later, the lift-to-drag ratio of a stationary wing deteriorates as the Reynolds number decreases. Due to the low weight and slower flight speed, a small flyer is substantially more influenced than large flyers by the flight environment such as wind gust. To overcome these challenges, natural flyers improve flight performance, including force generation and maneuverability, using flapping wings and wing-tail coordination. In particular, the fixed-wing design (other than the noticeable exam­ples such as the delta wing) tends to favor flow patterns with no large scale vortical flows, whereas flapping wing flyers, especially smaller species such as humming­birds and insects, generate coherent, large-scale vortical flows with low-pressure

regions. As discussed in detail in Chapter 3, several fluid flow mechanisms, including a leading-edge vortex caused by varying the AoA under dynamic pitch (induced either actively, by arm and muscle, or passively, by structural shape deformation) and spanwise flows associated with modest aspect ratios, among others, contribute to generating necessary lift and thrust. Of course, the movement of the wing, the substantial impact of wind gust and environmental uncertainty, and the associated structural deformation of the wing during flapping make flapping wing aerodynamics more complex and challenging to analyze.

In the next chapter, we summarize the rigid fixed-wing aerodynamics that shares fundamental aspects of low Reynolds aerodynamics such as flow separation, laminar- to-turbulent transition, and so on. In Chapter 3, we discuss rigid flapping wing aero­dynamics and focus on the wing kinematics and the resulting unsteady flow features involving flapping wings. In Chapter 4, we discuss aeroelasticity of flexible flapping wings including both active and passive mechanisms and implications.

As already mentioned, there are several prominent features of MAV flight: (i) low Reynolds numbers (104 to 105), resulting in degraded aerodynamic performance; (ii) small physical dimensions, resulting in much reduced payload capabilities and some favorable scaling characteristics including structural strength, reduced stall speed, and impact tolerance; and (iii) low flight speed, resulting in an order one effect of the flight environment such as wind gust, as well as intrinsically unsteady flight characteristics. The preferred low Reynolds number airfoil shapes are different in thickness, camber, and aspect ratio from those typically employed for manned air­craft. In this chapter, we discuss the low Reynolds number aerodynamics associated with rigid fixed wings, including the implications of airfoil shapes, laminar-turbulent transition, and unsteady free-stream on the performance outcome.

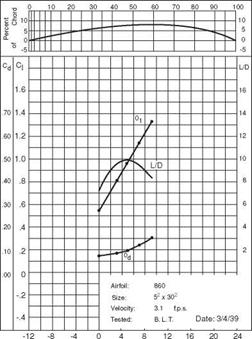
Schmitz [84] was among the first to investigate the aerodynamics for model airplanes in Germany, and he published his research in 1942. His work is often con­sidered to be the first reported low-speed wind-tunnel research. However, experi­mental investigations of low Reynolds number aerodynamics were conducted earlier by Brown [85] and by Weiss [86], in the two (and only) issues of The Journal of Inter­national Aeromodeling. Brown’s experiments focused on curved-plate airfoils, made by using two circular arcs meeting at a maximum camber point of 8 percent, but at varying locations. The wings’ test sections were all 12.7 cm x 76.2 cm, giving an AR of 6. In all cases, the tests were conducted at a free-stream velocity of 94 cm/s. The Reynolds number, although not mentioned in Brown’s study [85], is estimated to be about 8 x 103.

It is hard to judge the quality of the measurements reported in these early works (see Fig. 2.1). Nevertheless, these publications have clearly demonstrated that work with model airplanes offers much to scientific investigation and continues to generate enthusiastic inquiries about many aspects related to low Reynolds number aerodynamics. Representative figures from Brown’s experiments [85] are included here for us to gain a historical perspective.

Many published papers have improved our understanding and experimental database and have provided airfoil design guidance in the lower Reynolds number regime. For example, valuable insight has been offered by Liebeck [87], Selig et al. [88]-[90], and Hsiao et al. [91]. Liebeck [87] has addressed the laminar separation and airfoil design issues for the Reynolds number between 2 x 105 and 2 x 106, and

Hsiao et al. [91] have investigated the aerodynamic and flow structure of an airfoil, NACA 633-018, for the Reynolds number between 3 x 105 and 7.74 x 105. Selig et al. have reported on a wide variety of airfoils with basic aerodynamic data for the Reynolds number between 6 x 104 and 3 x 105 [88] [ 90] and for the Reynolds number between 4 x 104 and 3 x 105 [89]. In the following sections, we discuss the various aerodynamics characteristics and fluid physics for the Reynolds number between 102 and 106, with a focus on issues related to the Reynolds number of 105 or lower.