Derivation of the laminar boundary-layer equations

At high Reynolds numbers the boundary-layer thickness, 6, can be expected to be very small compared with the length, L, of the plate or streamlined body. (In aeronautical examples, such as the wing of a large aircraft 6)L is typically around 0.01 and would be even smaller if the boundary layer were laminar rather than turbulent.) We will assume that in the hypothetical case of ReL —> oo (where ReL = pUxLjp), <5 —> 0. Thus if we introduce the small parameter

1

“ ReL

we would expect that 6 —> 0 as є —> 0, so that

cx є

where n is a positive exponent that is to be determined.

Suppose that we wished to estimate the magnitude of velocity gradient within the laminar boundary layer. By considering the changes across the boundary layer along line AB in Fig. 7.7, it is evident that a rough approximation can be obtained by writing

du ^ Uao _ Uqq 1 dy~ 6 L є”

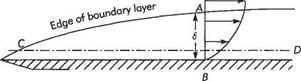
Fig. 7.7

Although this is plainly very rough, it does have the merit of remaining valid as the Reynolds number becomes very high. This is recognized by using a special symbol for the rough approximation and writing

dy

For the more general case of a streamlined body (e. g. Fig. 7.1), we use x to denote the distance along the surface from the leading edge (strictly from the fore stagnation point) and у to be the distance along the local normal to the surface. Since the boundary layer is very thin and its thickness much smaller than the local radius of curvature of the surface, we can use the cartesian form, Eqns (2.92a, b) and (2.93), of the Navier-Stokes equations. In this more general case, the velocity varies along the edge of the boundary layer and we denote it by Ue, so that

(7.3)

where Ue replaces иж, so that Eqn (7.3) applies to the more general case of a boundary layer around a streamlined body. Engineers think of G(Ue/6) as meaning order of magnitude of Ue/6 or very roughly a similar magnitude to Ue/6. To math – ematicans F = 0(1/єп) means that F oc l/є" as є —> 0. It should be noted that the order-of-magnitude estimate is the same irrespective of whether the term is negative or positive.

Estimating du/dy is fairly straightforward, but what about du/dxl To estimate this quantity consider the changes along the line CD in Fig. 7.7. Evidently, и = Ux at C and и —> 0 as D becomes further from the leading edge of the plate. So the total change in и is approximately!/«, — 0 and takes place over a distance Ax ~ L. Thus for the general case where the flow velocity varies along the edge of the boundary layer, we deduce that

(7.4)

Finally, in order to estimate second derivatives like d2u/dy2, we again consider the changes along the vertical line AB in Fig. 7.7. At В the estimate (7.3) holds for du/dy whereas at A, du/dy — 0. Therefore, the total change in du/dy across the boundary layer is approximately (U^/S) — 0 and occurs over a distance <5. So, making use of Eqn (7.1), in the general case we obtain

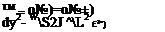cPu

In a similar way we deduce that

We can now use the order-of-magnitude estimates (7.3)-(7.6) to estimate the order of magnitude of each of the terms in the Navier-Stokes equations. We begin with the continuity Eqn (2.93)

One might question the assumption that two terms are the same order of magnitude. But, the slope of the streamlines in the boundary layer is equal to v/u by definition and will also be given approximately by b/L, so Eqn (7.8) is evidently correct.

0(Ul/L) 0{Xfi/L) dv dv з+ % – 0{ЄЧ/ЦЬ) 0{e*Ul/L)

+ -1^1 + *%) <7’9> O(unknown) 0(vUe/L2)=0(EU%/L) 0(i/£/e/(L2e2n))=0(Ei-2»U|/i)

We will now use Eqns (7.3)-(7.6) and (7.8) to estimate the orders of magnitude of the terms in the Navier-Stokes equations (2.92a, b). We will assume steady flow, ignore the body-force terms, and divide throughout by p (noting that the kinematic viscosity v = р/р), thus

Now є = 1/ReL is a very small quantity so that a quantity of 0(eU2/L) is negligible compared with one of 0(U%/L). It therefore follows that the second term on the right-hand side of Eqn (7.9) can be dropped in comparison with the terms on the left – hand side. What about the third term on the right-hand side of Eqn (7.9)? If 2л = 1 it will be the same order of magnitude as those on the left-hand side. If 2л < 1 then this remaining viscous term will be negligible compared with the left-hand side. This cannot be so, because we know that the viscous effects are not negligible within the boundary layer. On the other hand, if 2л > 1 the terms on the left-hand side of Eqn (7.9) will be negligible in comparison with the remaining viscous term. So, for the flat plate for which dp/dx = 0, Eqn (7.9) reduces to

c9u dy2

This can be readily integrated to give

u=f(x)y + g(x)

Note that, as it is a partial derivative, arbitrary functions of x, f(x) and g(x), take the place of constants of integration. In order to satisfy the no-slip condition (и = 0) at the surface, у = 0, g(x) = 0, so that и ос у. Evidently this does not conform to the required smooth velocity profile depicted in Figs 7.3 and 7.7. We therefore conclude that the only possiblity that fits the physical requirements is

2n = 1 implying 6 ос є1/2 -^L=)

and Eqn (7.9) simplifies to

du du

u—+ v— : dx dy

It is now plain that all the terms in Eqn (7.10) must be 0(el^2Ul/L) or even smaller and are therefore negligibly small compared to the terms retained in Eqn (7.12). We therefore conclude that Eqn (7.10) simplifies drastically to

dy

In other words, the pressure does not change across the boundary layer. (In fact, this could be deduced from the fact that the boundary layer is very thin, so that the streamlines are almost parallel with the surface.) This implies that p depends only on x and can be determined in advance from the potential-flow solution. Thus Eqn (7.12) simplifies further to

Equation (7.14) plus (7.7) are usually known as the (Prandtl) boundary-layer equations.

To sum up, then, the velocity profiles within the boundary layer can be obtained as follows:

(i)Determine the potential flow around the body using the methods described in Chapter 3;

(ii) From this potential-flow solution determine the pressure and the velocity along the surface;

(iii) Solve equations (7.7) and (7.14) subject to the boundary conditions

u = v = 0 at = 0; и = Ue at у — 6 (or oo)

The boundary condition, и = 0, is usually referred to as the по-slip condition because it implies that the fluid adjacent to the surface must stick to it. Explanations can be offered for why this should be so, but fundamentally it is an empirical observation. The second boundary condition, v = 0, is referred to as the no-penetration condition because it states that fluid cannot pass into the wall. Plainly, it will not hold when the surface is porous, as with boundary-layer suction (see Section 8.4.1). The third boundary condition (7.15) is applied at the boundary-layer edge where it requires the flow velocity to be equal to the potential-flow solution. For the approximate methods described in Section 7.7, one usually applies it at у = S. For accurate solutions of the boundary-layer equations, however, no clear edge can be defined;

the velocity profile is such that и approaches ever closer to Ue the larger у becomes. Thus for accurate solutions one usually chooses to apply the boundary condition at у = oo, although it is commonly necessary to choose a large finite value of у for seeking computational solutions.