Elementary Solutions for the Stream Function in Axisymmetric Flow

We now develop solutions for axisymmetric flow analogous to those described in Chapter 4.

Uniform Flow

Consider a uniform flow, VTC, in the x-direction in cylindrical coordinates. Then, from Eq. 7.20:

u =-1 dv = -1 f'(x) = 0 =>/( x) = constant.

r d x r

Arbitrarily setting у = 0 at r = 0 (i. e., along the x-axis), the stream function for uni­form flow is given by:

V r2

V = ^- (7.27)

As expected, lines of constant stream function (i. e., streamlines) are parallel to the x-axis. Recall from Chapter 4 that each streamline may be assigned a value corre­sponding to the volume (or mass) flux between it and a reference streamline. For planar, two-dimensional flow, у(x, y)~y, Ду(x, y) = Ay, and equal increments in mass flux are represented by straight lines equally spaced, as shown in Fig. 7.7a. For axisymmetric flow, equal increments in mass flux again are represented by straight lines parallel to the axis of symmetry, but these lines are not equally spaced in the x-r plane because Ду(*, r) = Ar2. Thus, for axisymmetric flow, lines of constant incre­ment in stream function become closer together as the distance, r, from the axis of symmetry increases, as illustrated in Fig. 7.7b.

Source Flow

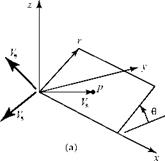
Consider a three-dimensional source at the origin of coordinates in three-space. One particular radial streamline from the source passes through any arbitrary point P(x, r) in any plane containing the x-axis and making an angle 9 with the у-axis, as shown in Fig. 7.8a. Now, we focus on one particular (x, r) plane (Fig. 7.8b) and recognize that

Figure 7.7. Constant increment in stream function, freestream flow.

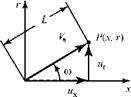Figure 7.8. Three-dimensional source flow in axial plane of symmetry.

because of the symmetry of the source flow field, the flow behavior in any such plane is independent of ю—that is, the source flow has axial (as well as spherical) symmetry.

In Fig. 7.8b, is the magnitude of the radial velocity at the point (x, r) due to a three-dimensional source at the origin of coordinates. From Eq. 7.25 this may be written as:

where K is a constant describing the source strength:

K = Л,

4 n

and L is the distance from the source to the point in question. Then, from Fig. 7.8b:

L = 4×2 + r 2

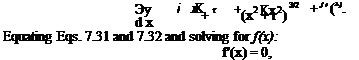Now, we take the derivative of Eq. 7.30 with respect to x, which yields:

which means that f(x) is a constant. Reflecting this in Eq. 7.30 and again setting у = 0 along the x-axis (r = 0), it follows that:

f (x) = , Kx = K = constant. six2 + 0

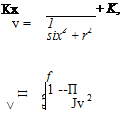Thus,

Eq. 7.34 represents the equation for the streamlines (у = constant) in any down­stream axial plane of symmetry due to the flow from a three-dimensional source at the origin of coordinates.