MISSILE AERODYNAMIC DERIVATIVES
TABLE 4.8
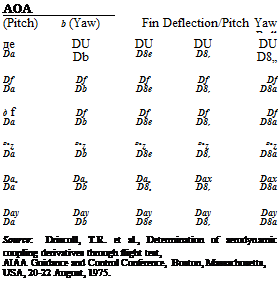
Missile Derivatives in a Linear Model
 Changes in Variables
Changes in Variables
Pitch angular acceleration
Roll angular acceleration Yaw angular acceleration Normal (pitch) acceleration, az Axial acceleration, ax Yaw acceleration, ay
by mass m and the moment derivatives are divided by respective moment of inertia. A complete linear derivative model of a missile could have 30 derivatives [9] as shown in Table 4.8.
Interestingly these derivatives of Table 4.8 are called acceleration derivatives. The reason will be clear from the following development:
8U _ pU2Sc 8a 2Iy ‘
We know from Equation 4.7 that
Hence, 8a = Ma and we see that the corresponding derivative is also called pitch angular acceleration derivative. Similarly, all other derivatives of Table 4.8 can be shown equivalent in their formats by their definitions to aircraft derivatives. Some additional derivatives seem to have been defined in the case of a missile as can be seen from the Table 4.8, as compared to aircraft.











