Munk’s Airship Theory

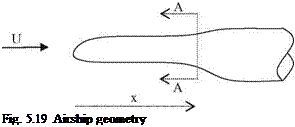
The aerodynamic forces acting on the airships first was given in a study made by M. M. Munk during the first quarter of the last century (Munk 1924). As we know from the physics of the problem, the rate of change of the momentum of the airflow normal to the freestream is equal to the force crated in that direction. Using this principle, first we can calculate the change of the momentum of the air displaced vertically by an arbitrarily shaped body as shown in Fig. 5.19. Let wa be the vertical velocity of the air parcel whose density is q, and S is the cross sectional area at a given station on the body. Since the cross sectional area changes with x, we denote the variables in their differential form as follows.

Let (pSdx) be the differential air mass displaced vertically with a mean velocity wa. Its differential momentum in z direction reads as

dIz = (pSdx)wa

Here, we assume the body is slender, therefore, we can take the mean vertical velocity value as the velocity of the axis of the body. Accordingly, if the position of the axis of the body is given with za = za(x, t) the vertical velocity reads as

0za 9za

Ot + Ox

The differential momentum of the air parcel then becomes

The rate of change of the momentum of the air is equal, but opposite in sign, to the vertical force acting in unit body length, i. e.,

dL D dIz

dx Dt dx

If we use Eq. 5.99 and assume that the air is incompressible for the cross flow, the vertical force for unit length becomes

If we assume that the cross section of the body does not change with time, and expand the substantial derivative in linearized form we obtain the lift change in x

Equation 5.100 is in very good with experiments performed for the slender bodies. Writing 5.100 for steady flow gives

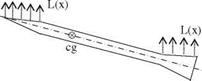Fig. 5.20 L(x) force acting on the slender body

According to Eq. 5.101, for steady flows, to have a differential force normal to the free stream we need to have for the body:

(i) an angle of attack and the cross sectional area change,

(ii) if the cross sectional area does not change then there has to be a camber!

Now, let us show the normal force L(x) acting on the slender body with angle of attack and the variable cross sectional area shown in Fig. 5.20 as a typical slender body shape. Using Munk’s theory, the aerodynamic force acting normal to the flight direction is at the front and back side of the body where there are cross sectional area changes. The same body does not experience any aerodynamical forces where the cross sectional area remains constant. The vertical forces may affect a short region on the body but the moment arms can be long, therefore effective pitching moments with respect to the center of gravity may be generated. These pitching moments, naturally, affect the stability of the body. One striking example to the unstable body is the one with the pointed nose and the pointed end where the forces create a continuous rotation about the center of gravity. The body shown in Fig. 5.20, on the other hand, has a flaired end to give a stable configu­ration (See Problem 5.32 for detailed description of stability criterion).