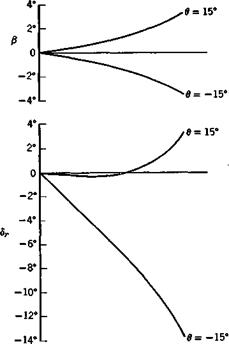
The values of [ft, dT, 6a] corresponding to low-speed flight at sea level (CL = 1, p = p0) for the jet transport of the previous examples have been calculated from (10.4,13) and are shown in Fig. 10.10. The numerical data and the aerodynamic coefficients are the same as in Secs. 9.6 and in the steady sideslip above. Both the sideslip angle and the rudder angle are seen to he very much dependent on в. This may be traced directly to the fact that the roll rate p is proportional to в and changes sign with it.
|
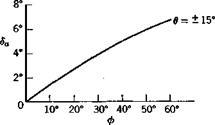
Fig. 10.10 Control angles in a truly banked turn.
|
|
Thus the term C nJp in the yawing moment equation is of opposite signs for climb and glide, and affects the rudder angle required to cancel the moment. Since Cy must also be zero, the value of /5 is in turn affected by that of 6r. One would expect that the difference in CtJ> between climbing and gliding would likewise cause a substantial difference between 6a for the two cases, whereas no such difference exists. It is fortuitous that in this example the term C^fj provides just the difference in the rolling moments needed.
Since ф > 0 represents a right turn, we see that the ailerons are deflected in the “off-bank” sense (stick left), that considerable right rudder is used for gliding turns, but that for climbing turns it may be in either direction.
Finally, it may be remarked that the control angles obtained would have been substantially different had it been stipulated that fl, not Cv, should be zero in the turn. It would not then be possible, however, to satisfy the requirement that the ball be centered in the turn-and-bank indicator.
|
|
|
|