NUMERICAL EXAMPLE—FREQUENCY RESPONSE

For this example we take the same hypothetical jet transport as was used in Sec. 9.1, flying at the same speed and height. For the aerodynamic transfer functions in P we use the stability derivative representation, i. e. all but Gm^ are the same as the corresponding stability derivatives, and Сгт(г — Gme + sCm ■. In addition, for the control aerodynamics we use

®LS = gls = -24/radian

GmS = Oms = — .72/radian

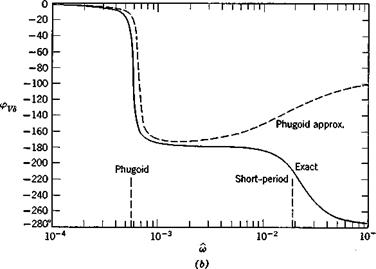
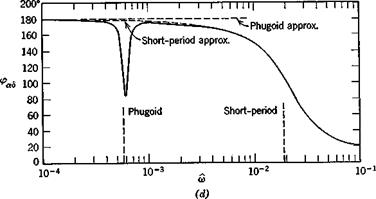
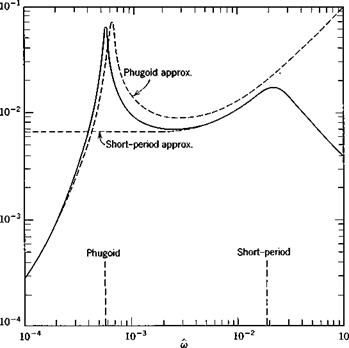
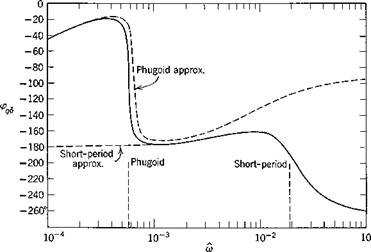
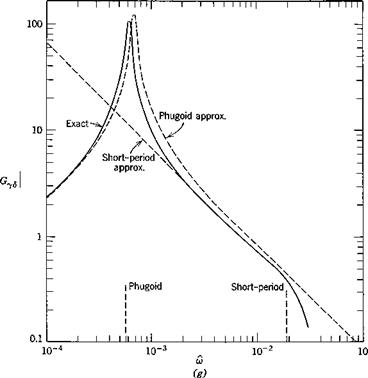
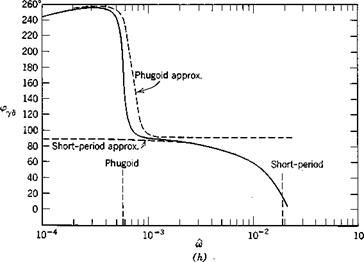
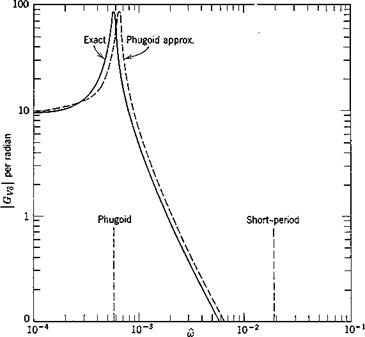
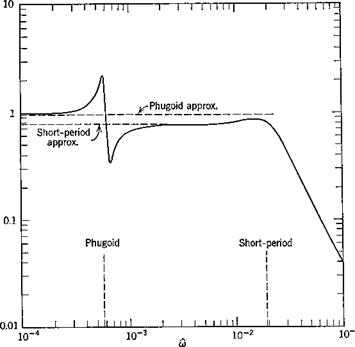
The exact frequency response was calculated from (10.2,1) and the two approximations from (10.2,11) and (10.2,15) by substituting s = ito in them. The results are shown on Fig. 10.3 for speed, angle of attack, and flight-path angle.

The exact solutions show that the responses in the “trajectory” variables V and у are dominated entirely by the large peak at the phugoid frequency. Because of the light damping in this mode, the dynamic gains at resonance are very large. The peak GVd of about 85 means that a speed amplitude of 10% of Ve would result from an elevator angle amplitude of only.1 X 57.3/85 = .068°. Similarly at resonance an oscillation of 10° in у would result from about 1/10° elevator amplitude. For both these variables, the response diminishes rapidly with increasing frequency, becoming negligibly small above the short-period frequency. The phase angle for V, Fig. 10.36, is zero at low frequency, diminishes rapidly to —180° at the phugoid frequency (very much like the lightly damped, second-order systems of Fig. 3.176) and subsequently at the short-period frequency undergoes a further drop char­acteristic of a heavily damped, second-order system. The “chain” concept of high-order systems (Sec. 3.4) is well exemplified by this graph.

By contrast, the attitude variables a and q show important effects at both the phugoid and short-period frequencies. The complicated behavior of a near the phugoid frequency indicates the sort of thing that can occur with high-order systems. It is associated with a pole and a zero of GaS occurring close together in the exact transfer function. Again, above the short-period frequency, the amplitude of a and q both fall off rapidly.

As to the approximate solutions shown, one general statement can be made. The short-period approximation is exact as m —> oo, and the phugoid approximation is exact as со —► 0. With a single exception, all the phenomena shown are represented reasonably well by one or other of the approximations. The exception is the oc response at the phugoid frequency, which is revealed only by the exact solution. The principal error in the approximations is the displaced peak at the phugoid. This corresponds to the error in the phugoid

(а)

Fig. 10.3 Frequency-response functions, elevator angle input. Jet transport cruising at high altitude, (a) Speed amplitude. (b) Speed phase angle, (c) Angle of attack amplitude, (d) Angle of attack phase angle, (e) Pitch-rate amplitude. (/) Pitch-rate phase angle, (g) Flight-path angle amplitude, (h) Flight-path angle phase angle.

(с)

Fig. 10.3. (Contd.)

(е)

(f) Fig. 10.3. (Gontd.) 412

Fig 10.3. (Contd.)

period shown for approximation (9.2,9) on Fig. 9.4a. Had the characteristic equation corresponding to (9.2,11) been used instead, the approximation would have been better.