NUMERICAL EXAMPLE—STEP RESPONSE

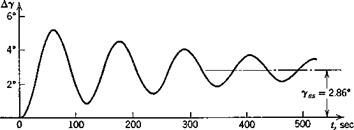
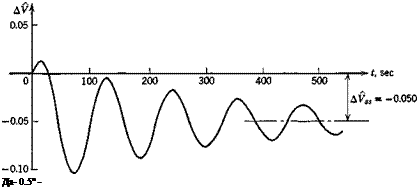
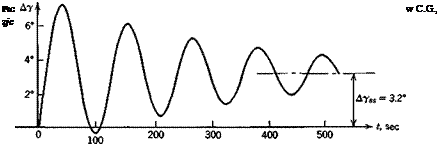
Analog computations were made for the airplane and flight condition of the previous example, with ДСТі_ = .0125 and with г/с = Oand.3 The results for F, a, and у are shown on Figs 10.7 and 10.8. The motion at this time scale is clearly dominated by the lightly damped phugoid. Consider Fig. 10.7

1—-

Aass = 0.29* —S – t, sec

(zjc = 0) first. We see that the speed begins to increase immediately, before the other variables have time to change. It then undergoes a damped oscil­lation, returning finally to its initial value. The angle of attack varies only slightly, and у makes an oscillatory approach to its final positive value yss. The ultimate steady state is a climb with Д1? = Да = 0, the numerical value of yss being correctly given by (10.3,4). For the case zjc = .3, Fig. 10.8, the results differ from the preceding in several significant ways. Although the speed does begin to increase at first, the increase is small and is quickly followed by a reduction of order 10% Ve. The final value is 5% less than Ve, a rather large change. The initial response in a is rapid, being dominated

by the short-period mode, and is not seen in detail at this time scale. Because of the rapid increase in a, and the excess lift that goes with it, there is a much more rapid response in y. than is the case in Fig. 10.7. The amplitude of the у oscillation is also larger than on Fig. 10.7, and the final state is a climb of appreciably larger inclination. The steady states are again correctly predicted by (10.3,3).