Numerical Methods for Uncertainty Quantification and Bayesian Update in Aerodynamics
Alexander Litvinenko and Hermann G. Matthies
Abstract. In this work we research the propagation of uncertainties in parameters and airfoil geometry to the solution. Typical examples of uncertain parameters are the angle of attack and the Mach number. The discretisation techniques which we used here are the Karhunen-Loeve and the polynomial chaos expansions. To integrate high-dimensional integrals in probabilistic space we used Monte Carlo simulations and collocation methods on sparse grids. To reduce storage requirement and computing time, we demonstrate an algorithm for data compression, based on a low – rank approximation of realisations of random fields. This low-rank approximation allows us an efficient postprocessing (e. g. computation of the mean value, variance, etc) with a linear complexity and with drastically reduced memory requirements. Finally, we demonstrate how to compute the Bayesian update for updating a priori probability density function of uncertain parameters. The Bayesian update is also used for incorporation of measurements into the model.
1 Introduction
Nowadays, the trend of numerical mathematics is often trying to resolve inexact mathematical models by very exact deterministic numerical methods. The reason of this inexactness is that almost each mathematical model of a real world situation contains uncertainties in the coefficients, right-hand side, boundary conditions, initial data as well as in the computational geometry. All these uncertainties can affect the solution dramatically, which is, in its turn, also uncertain. The information of the interest is usually not the whole set of realisations of the solutions (too much data), but some other stochastic information: cumulative distribution function, probability density function, mean value, variance, quantiles, exceedance probability etc.
Alexander Litvinenko • Hermann G. Matthies
Institute of Scientific Computing, Technische Universitat Braunschweig, Hans-Sommer str. 65, 38106, Braunschweig, Germany e-mail: wire@tu-bs. de
http://www. wire. tu-bs. de
B. Eisfeld et al. (Eds.): Management & Minimisation of Uncert. & Errors, NNFM 122, pp. 265-282. DOI: 10.1007/978-3-642-36185-2_11 © Springer-Verlag Berlin Heidelberg 2013
During the last few years, one can see an increasing interest in numerical methods for solving stochastic computational fluid dynamic (CFD) problems [3, 8, 17, 19, 24, 26]. In this work we consider an example from aerodynamics, described by a system of Navier-Stokes equations with a k-w turbulence model. Uncertainties in parameters such as the angle of attack a and Mach number are modelled by random variables, uncertainties in the shape of the airfoil are modelled by a random field [14, 12]. Uncertain output fields such as pressure, density, velocity, turbulence kinetic energy are modelled by random fields as well. The lift, drag and moments will be random variables.
We assume that there is a solver which is able to solve the deterministic (without uncertainties) Navier-Stokes problem. In this work we used the TAU code (developed in DLR) with k-w turbulence model [4]. We also assume that spatial discretisation of the airfoil is given. Our job is the appropriate modelling of uncertainties and developing stochastic/statistical numerical techniques for further quantification of uncertainties. At the same time, due to the high complexity of the deterministic solver, we are allowed to use only non-intrusive stochastic methods such as Monte Carlo or collocation methods. So, we are interested in methods which do not require changes in the deterministic code.
The rest of the paper is structured as follows. In Section 3 we describe the problem and discretisation techniques, such as the Karhunen-Loeve expansion (KLE) [16] and polynomial chaos expansion (PCE) of Wiener [25]. In Section 2.1 we explain how we model uncertainties in the parameters angle of attack and Mach number. Uncertainty in the airfoil geometry is described in Section 2.2. The low-rank response surface is presented in Section 4. To avoid large memory requirements and to reduce computing time, low-rank techniques for representation of input and output data (solution) were developed in Section 5. Section 7 is devoted to the numerical results, where we demonstrate the influence of uncertainties in the angle of attack a, in the Mach number Ma and in the airfoil geometry on the solution – drag, lift, pressure and absolute friction coefficients. The strongly reduced memory requirement for storage stochastic realisations of the solution is demonstrated as well. In Section 6 we demonstrate how to use the Bayesian update (BU) for improving the statistical description of the random airfoil geometry. Section 7 is devoted to other numerical experiments.
2 Statistical Modelling of Uncertainties
The problem to consider in this work is the stationary system of Navier-Stokes equations with uncertain coefficients and parameters:
v(x, co) ■ Vv(.r, со) – ^V2v(.r, со) + Vp{x, со) = g(x) хє&, со e Q V • v(x, ю) = 0
|
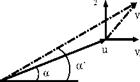
u
|
Fig. 1 Two random vectors vj and V2 model free-stream turbulence, u and u old and new free stream velocities, a and a old and new angles of attack with some initial and boundary conditions. Here v is velocity, p pressure and g the right-hand side, the computational domain G is RAE-2822 airfoil with some area around. Examples of uncertain parameters are the angle of attack a and the Mach number Ma. Uncertainty in the airfoil geometry is modelled via random field (see Section 7).