Numerical Stability

All numerical schemes are liable to be numerically unstable. One can usually avoid numerical instability by taking an appropriately small At. The numerical stability requirement of the DRP scheme will now be investigated. Recall that the Fourier – Laplace transform of the DRP scheme is formally the same as that of the original Euler equations (with a, в, m replaced by a, в, M, respectively). Thus, by modifying Eq. (5.18) accordingly, the pressure associated with the acoustic waves computed by the DRP scheme is given by

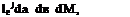
[p0^2(aG2 + в G3) + (m — au0)G4
(M — au0 )2 — «2 (a2 + в2)

(5.39)

where a (a), в(в), and m(m) and its inverse m = m(m) are given by Eqs. (2.9) and (3.16). From the theory of Laplace transform, it is well known that for large t the dominant contribution to the м-integral comes from the residue of the pole of the integrand that has the largest imaginary part in the complex м plane. In Eq. (5.39), the pole corresponding to the outgoing acoustic wave is given implicitly by

m(m) = a(a)u0 + a0(a2(a) + в (в))2. (5.40)

As discussed in Chapter 3, for a given M, there are four values of m. Thus, there are four wave solutions associated with the M pole of dispersion relation (5.40);

three of which are spurious. Let the roots be denoted by ok (k = 1, 2, 3, 4) with corresponding to the physical acoustic wave. On completing the contour in the lower half ю plane by a large semicircle, by the Residue Theorem, the pressure field given by Eq. (5.39) becomes

4

p(x, y, t) = Y^ – (2ni)

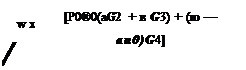k=1

To obtain numerical stability, a sufficient condition is

Im(юk) < 0, к = 1, 2, 3, 4. (5.42)

Note, from Figure 2.3, that for arbitrary values of a and в the inequalities

a Ax < 1.75, pAy < 1.75 (5.43)

hold true. Substitution of inequality (5.43) into Eq. (5.40), and upon multiplying by A t, it is found that

where M is the Mach number. From Figure 3.1 it is clear that if |OAt| is less than 0.41, then all the roots of ok, especially the spurious roots, are damped. Therefore, to ensure numerical stability, it is sufficient by Eq. (5.44) to restrict At to less than

where Atmax is given by

Similar analysis for the entropy and the vorticity wave modes of the finite difference scheme yields the following criterion for numerical stability:

Formula (5.45) is a more stringent condition than formula (5.46). Therefore, for At < Atmax, the DRP scheme would be numerically stable.