Optimum unswept wing
It is useful to first consider an unswept wing. We therefore assume
ce = Cl
![]()
![]() cd(ce, M’x>)
cd(ce, M’x>)
Cl
^t^wing ^ У)’ ^ ^West where CDwing is the wing’s profile+wave drag, and CDrest is the profile drag of the remaining fuselage, tail, and nacelle components. The objective is to find the optimum Cl, MTO combination which minimizes the Cd/МЦ2Cl fuel-burn parameter. For a numerical example we can pick
AR = 10 , CDrest = 0.025
which are typical for modern jet transports. Using the 2D 12%-thick airfoil Cd Mach drag-rise sweeps shown in Figure 8.34, the corresponding fuel-economy parameters are shown in Figure 8.35. The optimum combination is roughly at
Cl = 0.8 , MTO = 0.725 (unswept-wing optimum)
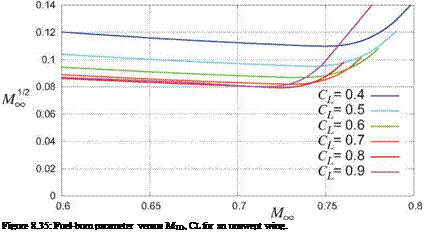 |
although this will also depend on the airfoil thickness. A larger thickness will typically optimize to a lower Cl and a lower MTO, with a corresponding increase in the fuel-burn parameter. However, a thicker wing is structurally favorable and hence lighter, so that the WZF factor in the Breguet relation (8.175) may overcome this aerodynamic drawback and give a net benefit.
Swept-wing airfoil characterization
The earlier analysis of an infinite swept wing in Section 8.6.3 indicated that the lift depends only on the perpendicular velocity and Mach component V± = V» еовЛ and M± = MTO еовЛ. The same arguments apply to the airfoil’s boundary layers, provided we ignore the spanwise flow’s increase of the total-velocity
Reynolds number, which is reasonable for fully-turbulent flow. Consequently, the 2D airfoil lift-coefficient characteristics shown in Figure 8.34 apply to a swept wing via the following relations.
![]() Ml = M, cos Л ce = Cl± = Cl/ cos^
Ml = M, cos Л ce = Cl± = Cl/ cos^
Cd = Cd(ce; Ml)
To obtain the wing’s profile drag coefficient CDwi from the 2D-section Cd value we first break down the latter into the friction and pressure components,
Cd = Cdf + Cdp (8.179)
with a roughly |, | split, respectively, being typical for transonic airfoils.
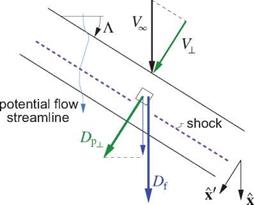
The velocity within the 3D boundary layer on the wing and hence the surface skin friction vectors Tw will be mostly aligned with the outer potential flow, which is on average parallel to the freestream velocity V, and hence the aircraft’s X direction, as indicated in Figure 8.36. This skin friction’s magnitude must also scale with the local potential-flow dynamic pressure, which scales with the freestream dynamic pressure j>.. I ‘2. This gives the following estimate for the wing’s friction drag vector.
![]() Dfx = TwdS ~ pooV^Scdiyi
Dfx = TwdS ~ pooV^Scdiyi
In contrast, the pressure forces act along the wing surface normal vectors n which lie in the plane perpendicular to the wing, so the pressure drag vector must be along the local chordwise vector X’ which lies in this plane. It must also scale as (>.. V2, since it must vanish in the limit of purely-spanwise flow at 90° sweep.
 |
|
 |
|
Dp± Xу = ff-pn dS ~ S cdp x’ = pccV2 S cdp cos2A x’ (8.181)
Figure 8.36: Profile drag of swept wing estimated from airfoil-plane friction and pressure-drag coefficients.
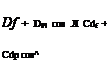 |
||
The total wing profile drag and corresponding drag coefficient are then
so that the wing’s overall profile-drag to lift ratio is
![]() Cbwing = Cdf + Cdv cos3A Cl cg ео82Л
Cbwing = Cdf + Cdv cos3A Cl cg ео82Л
which increases monotonically with sweep if 2Cdt > Cd which is invaiiably the case in the absence of significant flow separation. Hence, wing sweep by itself does not improve the wing’s drag/lift ratio, and in fact decreases it. The fuel-burn benefit from sweep instead originates from the speed/efficiency characteristics of jet engines, considered next.
Optimum swept wing
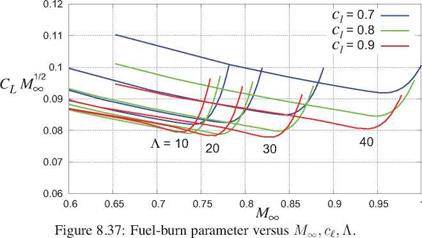
Sweep introduces another design parameter into the wing design space, which is now {Cl, M00, Л}, and also includes the airfoil thickness if different airfoils are being considered. The airfoil coefficients with the above sweep corrections give the fuel-burn parameter in the form
which is shown in Figure 8.37. The optimum design-parameter combination is now
cg = 0.9 , MTO = 0.825 , Л = 30° (swept-wing optimum)
and the corresponding fuel-burn parameter value of about 0.078 is smaller than the 0.080 value for the unswept-wing case shown in Figure 8.35 for a typical supercritical airfoil. The reduction is modest, but perhaps more importantly it occurs at a 0.825/0.725 — 1 = 14% greater speed which itself has economic benefits.
 |
The optimum design parameters found here for the swept-wing case are quite close to what’s seen on most modern jet transports, with the exception of the cg value. In practice, lower values of cg ~ 0.75 are used for several reasons: 1) Because of local cg reductions near the wingtips, wing root, and over the fuselage, the actual airplane Cl is necessarily smaller than the infinite swept-wing value cg еов2Л. 2) Structural weight considerations favor thicker airfoils than what this aerodynamic-only optimization indicates, and thicker transonic airfoils have lower optimum cg values.













