PHUGOID APPROXIMATION

The phugoid approximation in Sec. 9.2 was based on the assumption that Да is negligibly small and the pitching moment equation is identically satisfied. When the elevator angle is varying however, Да can no longer be assumed small. The equivalent assumption for this case is that pitch equilibrium is maintained, i. e. that

Aa + Gmaq + Gmd A3e = 0

Now we expect this approximation to be useful only at low elevator fre­quencies, when we can replace the above expression by

Gm<z Aa + Gmfl + Gmg Ade = 0

We now further assume that Gm<q is negligible, so that the angle of attack is given by the quasistatic value

Q

Да =——– — A3e (10.2,13)

Gm

The usefulness of this assumption is checked a posteriori. With the pitch equation eliminated from (10.2,1) and Да eliminated by (10.2,13), we get the reduced system equation

GTr — 2/is	0	1 О ___ 1	AV
■~2CWe	2/л	0	й	=	GLg-G-^(GLa + GDe + 2Ms) °ma	A 3e
_ 0	1	—s _	_A0_		_ 0 _

(10.2,14)

The required basic transfer functions are obtained from (10.2,14) as

~GLpW. + Tp [GWe(GLx + GD) + 2/“CxyS]

A ^

GVS — —————– 2 2 7Г~7І T~o7I 2—————————- (a)

4/i s — 2fiCTys + 2CWe

-GaGTV – ^ [-2aW'(CW’ – C^)

G + Gtv(glx + CID.) + 2у(СТг – glx – gd) ~ V*2]

ва 4/A2 – 2fiGTys + 2GW*

д 6 (Ь) (Ю.2Д5)

= (c)

From (10.2,13) we have in addition

A °ms . mct	(d)
and finally
G7S = G0S ~ GaS	(e)

As expected, the denominators of (10.2,15a and b) give the same characteristic equation as was used for the phugoid previously, i. e. (9.2,9).

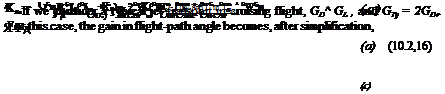The assumptions on which (10.2,15) are based hold exactly in the limit of zero control frequency, and hence the static gains given by them are correct. Taking the limit s —► 0 (see (3.2,4)) we get the gains

C/’/j / (/7) От

,,0’2’17)

The interesting thing about (10.2,17) is that it can change sign as GWe ( = CLJ

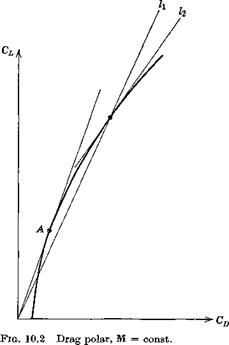
varies. With reference to Fig. 10.2 the quantity in parentheses on the r. h.s., for constant Mach number, can be written

dOD

where dCLjdCD is the slope of the tangent to the drag polar, l2. Since CLICD is the slope of l1; it is evident that (GDjGL)(dGLldGD) is unity at point A, is <1 for Gl > GLa and >1 for CL < GLa. As a result the second term on the r. h.s. of (10.2,17) is negative for CL < CL and positive for CL > GLa. Because of the first term in (10.2,17) К s does not change sign exactly at A, but at a slightly lower value of CL. With typical numerical values KyS= 0 when (CBjGL)(dCjjdCD) == 1.05. The point of all this is that A represents flight at (L/D)max, or at minimum drag, and hence that the ultimate response of flight-path angle to elevator reverses when this speed is crossed. At high speed (low CLJKyS is negative, so that up-elevator (stick back) produces a climb, but at low speed the opposite occurs. This result is seen to be entirely compatible with the conclusions reached from performance considerations, see Fig. 10.1. It is seen that the sign of Г — D for a speed reduction (associ­ated with a negative A. de) is opposite for points P and Q on opposite sides of the minimum-drag speed.