Prediction of In-Flight Airloads

While it has been shown previously that the problem of dynamic stall can be conveniently dissected, analyzed, and modeled into more manageable subproblems, it is only when the elements of the submodels are combined into the full rotor simulation, including the rotor wake (inflow) and elastic blade dynamics, that the true benefits of any improved modeling efforts can be realized. Many authors have shown the effects of including representations of dynamic stall for rotor loads and aeroelastic predictions – see, for example, Tarzanin (1972), Gormont (1973), Johnson (1969, 1974), Carlson et al. (1974), Yen & Yuce (1992), and Nguyen & Johnson (1998). The predicte results are, however, somewhat mixed. Generally, by including unsteady aerodynamics and dynamic stall models, better predictions of the phasing of the unsteady airloads with respect to blade azimuth are obtained, along with correspondingly better predictions of overall rotor performance at the extremes of the flight envelope. However, the mixed results indicate that although it may be possible to reproduce the unsteady airloads on a 2-D section with most dynamic stall models, the prediction of in-flight airloads are much more difficult.

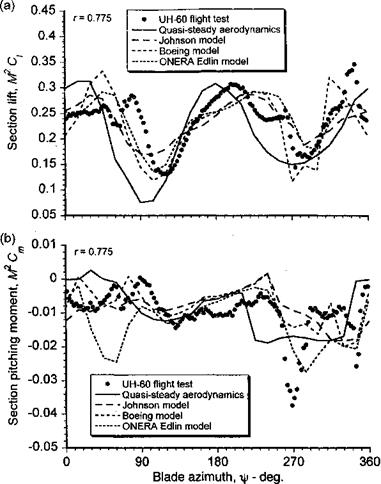
A representative example is shown in Fig. 9.18, which shows the lift (as M2Ci) and the pitching moment (as M2Cm) on a section of a rotor blade for a case where dynamic stall is present. The flight test results are taken from Bousman (1998), and the calculated results are taken from Nguyen & Johnson (1998). The unsteady airloads are computed with different dynamic stall models, while keeping fixed all other elements of the rotor model. As seen from Fig. 9.18, the agreement of the predictions with the measurements is indeed very mixed. The improvement over the use of quasi-steady aerodynamics is, however, clearly better, particularly in regard to the phase of the lift predictions. However, the predictions of the section pitching moment are probably less than what would be considered acceptable. For example, one of the models predicts large nose-down moments associated with dynamic stall at points over the disk where there is clearly no stall indicated in the flight test measurements. In other cases, stall is not predicted in the regions where flight tests clearly indicate otherwise.

The fault, however, lies not only with the stall models. The main difficulty in the rotor simulation is the proper calculation of the combination of AoA and Mach number that

will delimit attached flow, and these calculations must properly include models of the rotor wake and blade motion in a fully coupled way. Because of the high AoA gradients that exist over the disk resulting from the wake inflow (see Fig. 3.30), the time steps (level of discretization) used in the rotor analysis can determine whether or not dynamic stall is initiated at all. In other words, it is possible to completely miss the stall event because the time step is too large to resolve the phenomenon. Furthermore, vortex shedding during dynamic stall occurs over relatively short time scales, generally of the order of 8 semi­chords of airfoil travel – see Galbraith et al. (1986). Therefore, if translated into an azimuth step for the rotor calculation, the azimuth step must be of the order of 2—5° to accurately represent dynamic stall. In the calculations shown in Fig. 9.18, a rotor azimuth step of 15° was used, which is probably too large to capture the correct details of stall onset and subsequent aft center of pressure movement resulting from dynamic stall. Therefore, this level of predictive capability is of great concern to the rotor analyst and shows that even if the ability to model 2-D (or even 3-D) unsteady airloads has been realized, the prediction of dynamic stall airloads in the rotor environment is still a problem that is at the limit of

current modeling capabilities. Equivalent arguments apply for phenomena such as blade vortex interaction (BVI), which occur over time scales of the order of 2-5 semi-chords of airfoil travel. In this case, the time (azimuth) step must be of the order of one degree or less to resolve both the wake and the BVI phenomena. Trading off predictive capability of the physics against computational cost is never a good situation, but this is slowly changing. The answer, however, does not just lie in the need for bigger and faster computers, but in better solution algorithms that have the accuracy and stability suitable for application to smaller spatial and temporal discretizations needed for high-fidelity helicopter rotor aerodynamic simulations.