RESPONSE TO ELEVATOR INPUT

For the conventional case of cruising flight of airplanes, (5.14,2) can be used for the response to elevator by setting ДQT^ = 0. We shall first make some simplifying assumptions, i. e. that ocr = 0, that the reference flight path is horizontal, soye = 0, and that all oiGDV, GLV, GmV, Gj^ are negligible. It is assumed further that deflecting the elevator can change the lift and moment, but not the drag, so that ACDc = 0, ACLc = Gj^ Ade and AGmc = Gmi Ad„. Then (5.14,2) reduces to

(10.2,1)

The aerodynamic transfer functions on the r. h.s well enough by (see Sec. 5.14)

= °LS

G/iia ‘ ■ Gma “I – sGm^

and Gm-a is furthermore frequently neglected.

Let the 4×4 matrix on the l. h.s. of (10.2,1) be denoted P. Then (10.2,1) may be compactly written

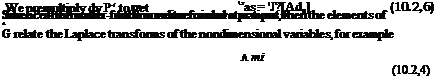The above elements of G do not exhaust the transfer functions of interest. Other response quantities may be wanted—for example, the flight-path angle and the normal load factor. The former is given by у = в — a, so that

Gyd = Ова ~ &*а (10-2,7)

The latter (see Sec. 6.10) is

L

n = —

W

and is unity in the reference condition. The perturbation in n is

An = — = — (ACL + 2Gl AV) (10.2,8)

wcWe L L*

to first order. ACL is conveniently expressed in terms of the state variables as

= glv AF + 6La Да + djJ[ + GLSA6e

After substituting in the Laplace transform of (10.2,8), and dividing by A6e we get

The preceding equations can be used directly for machine computation of frequency response functions, which basically requires only routine operations on matrices with complex coefficients; an example of this appli­cation is given below. However, for analysis one needs the literal expressions for the various transfer functions, and in some applications one must also find their inverse (the impulse response functions). This is not a practical analytical procedure for the complete system, even with the simplified equation (10.2,1). For obtaining exact solutions for the impulse response or step response, the preferred method is to solve the original differential equations on a digital or analog computer. For analytical work associated with control system design, approximate forms of the transfer functions may be quite useful (refs. 9.4 and 9.5).

We can find approximate transfer functions by using the short-period and phugoid approximations given in Sec. 9.2 as a guide. These would be expected to be useful for inputs whose spectral representations are limited to certain frequency bands appropriate to the mode in question.