A GENERIC EXAMPLE

For the sake of clarity, the method is introduced with the following gen­eric example. Let G(s, 6) the uncertain plant model, i. e. aMIMO transfer matrix which depends on a vector 8 of parametric uncertainties. Follow­ing chapter 3, G(s,8) can be transformed into an LFT Fi(P(s), Ai), where:

is a model perturbation with real possibly repeated scalars <5*.

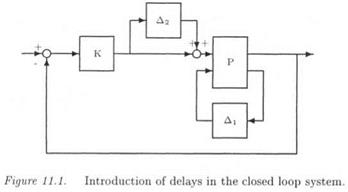
Controller K(s) is connected with G(s,8) and a model perturbation Д2(з) is added at the plant inputs (see Figure 11.1). Д2(з) represents the uncertain time delays:

Д2(в) = diag(e~ns — 1,…, e~TNS — 1) (11.4)

This uncertain closed loop is finally transformed into the standard in­terconnection structure M(s) – A(s). M(s) is simply the transfer matrix seen by the model perturbation A(s) = diag(Ai, ДгЫ) in the closed loop of Figure 11.1.

Remark: other examples could be considered, since other sources of parametric uncertainty or neglected dynamics could be introduced at various points of the closed loop (see chapter 1). Time delays could be moreover introduced at the plant outputs, in order to take into account delays in the sensors. The key issue is to obtain the standard intercon­nection structure M(s) – A(s),with A(s) = diag(Ai(s), A2(s)). Ai(s) is a mixed model perturbation gathering all classical model uncertainties (parametric uncertainties and neglected dynamics), whereas the model perturbation ДгЫ contains all uncertain time delays.

The robust delay margin is now defined in the specific context of the example. Assume that each parametric uncertainty Si is normalized, so that the vector S = (й)іє[і, м] belongs to the unit hypercube:

D = {6 – 1 < Si < 1 Vi Є (11.5)

A specific value of 6 is applied to the closed loop of Figure 11.1. Let Дт(<5) the MIMO delay margin associated to this closed loop: this means that the robust stability of the closed loop is guaranteed for all values of time delays Tj inside the interval [0, Дт(£)]. The robust MIMO delay margin At* is then defined as the minimal value of Дт(<5) over the unit hypercube[11]:

At* = min Дт(5) (11,6)