Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
AERODYNAMIC LOADS
Once Eq. (9.25) is solved the unknown singularity values are obtained (цк in this example). The velocity components are evaluated now in terms of the panel local coordinates (l, m,n) shown in Fig. 9.10. The two tangential perturbation velocity components are
_ dfi dfi
q,~~3l =
where the differentiation is done numerically using the values on the neighbor
FIGURE 9.10
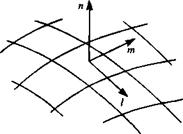Panel local coordinate system for evaluating the tangential velocity components.
panels. The normal component of the velocity is obtained from the source (in this example):
qn = – o (9.27)
The total velocity in the local (/, m, n) direction of panel к is
Q* = (Qoo,, Qocm, <2=0* + (qh qm, q„)k (9.28)
 |
 |
 |
and of course the normal velocity component on a solid boundary is zero. The pressure coefficient can now be computed for each panel using Eq. (4.53):
 |
The contribution of this element to the nondimensional fluid dynamic loads is normal to the panel surface and is
|
AC* |
 |
 |
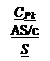where S is a reference area. In terms of the pressure coefficient the panel contribution to the fluid dynamic load becomes
The individual contributions of the panel elements now can be summed up to compute the desired aerodynamic forces and moments.
