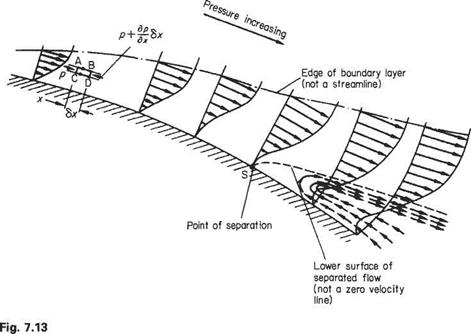
Boundary-layer separation

The behaviour of a boundary layer in a positive pressure gradient, i. e. pressure increasing with distance downstream, may be considered with reference to Fig. 7.13. This shows a length of surface that has a gradual but steady convex curvature, such as the surface of an aerofoil beyond the point of maximum thickness. In such a flow region, because of the retardation of the mainstream flow, the pressure in the main­stream will rise (Bernoulli’s equation). The variation in pressure along a normal to the surface through the boundary-layer thickness is essentially zero, so that the pressure at any point in the mainstream, adjacent to the edge of the boundary layer, is transmitted unaltered through the layer to the surface. In the light of this, consider the small element of fluid (Fig. 7.13) marked ABCD. On face AC, the pressure is p, while on face BD the pressure has increased to p + (dp/dx)6.x. Thus the net pressure force on the element is tending to retard the flow. This retarding force is in addition to the viscous shears that act along AB and CD and it will continuously slow the element down as it progresses downstream.

This slowing-down effect will be more pronounced near the surface where the elements are more remote from the accelerating effect, via shearing actions, of the mainstream, so that successive profile shapes in the streamwise direction will change in the manner shown.

Ultimately, at a point S on the surface, the velocity gradient (du/dy)w becomes zero. Apart from the change in shape of the profile it is evident that the boundary layer must thicken rapidly under these conditions, in order to satisfy continuity within the boundary layer. Downstream of point S, the flow adjacent to the surface will be in an upstream direction, so that a circulatory movement, in a plane normal to the surface, takes place near the surface. A line (shown dotted in Fig. 7.13) may be drawn from the point S such that the mass flow above this

line corresponds to the mass flow ahead of point S. The line represents the continuation of the lower surface of the upstream boundary layer, so that, in effect, the original boundary layer separates from the surface at point S. This is termed the separation point.

Reference to the velocity profiles for laminar and turbulent layers (Fig. 7.4) will make it clear that, owing to the greater extent of lower-energy fluid near the surface in the laminar boundary layer, the effect of a positive pressure gradient will cause separation of the flow much more rapidly than if the flow were turbulent. A turbulent boundary layer is said to stick to the surface better than a laminar one.

The result of separation on the rear half of an aerofoil is to increase the thickness of the wake flow, with a consequent reduction in the pressure rise that should occur near the trailing edge. This pressure rise means that the forward-acting pressure force components on the rear part of the aerofoil do not develop to offset the rearward­acting pressures near the front stagnation point, in consequence the pressure drag of the aerofoil increases. In fact, if there were no boundary layers, there would be a stagnation point at the trailing edge and the boundary-layer pressure drag, as well as the skin-friction drag, would be zero. If the aerofoil incidence is sufficiently large, the separation may take place not far downstream of the maximum suction point, and a very large wake will develop. This will cause such a marked redistribution of the flow over the aerofoil that the large area of low pressure near the upper-surface leading edge is seriously reduced, with the result that the lift force is also greatly reduced. This condition is referred to as the stall. A negative pressure gradient will obviously have the reverse effect, since the streamwise pressure forces will cause energy to be added to the slower-moving air near the surface, decreasing any tendency for the layer adjacent to the surface to come to rest.