Discrete panel method for a general wake

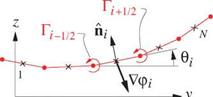
For a general wake shape, the force integrals must be evaluated using numerical integration. A relatively sim­ple method is to discretize the wake into i = 1. ..N panels as shown in Figure 5.12, with each panel i hav­ing a length A Si, and a piecewise-constant potential jump Api, The sideforce and lift integrals (5.64),(5.65) then become sums over all the panels. The convenient panel inclination angle 9i is also introduced, so that

Ayi = cos 9i Asi and Azi = sin 9i Asi.

Figure 5.12: Wake paneling for evaluation of Trefftz-plane forces.

To evaluate the induced drag integral (5.47) it is necessary to first determine the normal velocity Vpi ■ ni at each panel midpoint. This is the velocity of all the trailing vortices resulting from the discrete steps in the potential jump. Referring to Figure 5.12, each trailing vortex strength is

ri — 1/2 — Api — 1 Api

defined positive about the x axis, or counterclockwise in the yz plane. The velocity at each panel midpoint is then the discrete counterpart of the 2D velocity superposition (5.38).

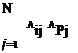Its normal component can then be condensed into a convenient Aerodynamic Influence Coefficient (AIC) matrix Aij which depends only on the wake geometry,

and allows calculation of др/диг for any panel Aрг distribution by the simple summation. The induced drag integral (5.47) is then approximated by a second sum over the panels.

1 ^ д

Di = –p^^ALpi-^-Asi (5.82)

i= 1 г