EXAMPLE—SUPPRESSION OF THE PHUGOID

The characteristic lightly damped, low-frequency oscillation in speed, pitch attitude, and altitude that was identified in Chapter 9, was seen in Chapter 10 to lead to large peaks in the frequency-response curves (Fig. 10.3) and long transients (Figs. 10.6 and 10.7). Similarly, in the control-fixed case, there are large undamped responses in this mode to disturbances such as atmospheric turbulence (see Chapter 13). These variations in speed, height, and attitude are in fact not in evidence in actual flight; the pilot (human or automatic) effectively suppresses them, maintaining flight at more or less constant speed and height. The logic by which this process of suppression takes place is not unique. In principle it can be achieved by using feedback signals derived from any one or a combination of pitch attitude в, altitude zE, speed V, and their derivatives. In practice, the availability and accuracy of the state information determines what feedback is used. We shall see that a simple negative feedback of pitch attitude suffices effectively to eliminate the phugoid. Pitch attitude is instantly and accurately available from either the real or artificial horizon. We shall also see that operating on speed error can produce pitch maneuvers free of phugoid oscillations.

Consider the system shown in Fig. 11.2, in which dc is the pitch command,

Fig. 11.2 Phugoid suppression system.

Gp(s) is the overall transfer function of the control system, and g is a dis­turbance (gust) input. The pitch attitude is given by

e = G9gg + Ges5e (11.2,1)

and we readily find the overall transfer functions

0 g, Qw

0C 1 + GvGes

0 Q»t

9 1 + GvGei

The stability with respect to 6C or g inputs is given by the roots of the char­acteristic equations of these two overall transfer functions. So long as de and g are both inhomogeneous inputs to the linear aircraft system, it can be seen that the denominators of Ges and Geg are the same, each being the char­acteristic polynomial det (si — A) (see Sec. 3.2). Thus we may write

where Nv N2, D are polynomials in s, and the overall transfer functions are

0 GvN1

вс D + GI1N1
g D + GVNX

The poles of these transfer functions, which are the roots of the characteristic equations, will be the same if GpN1 and N2 have no poles (or the same poles), and in that case the stability with respect to gust inputs will be the same as that for pitch command inputs. A reasonably general form for Gp(s) for this application is

<?»(*) = -1 + h + h*

s

For obvious reasons, the three terms on the r. h.s. are called, respectively, integral control, proportional control, and rate control, because of the way they operate on the error e. The particular form of the controlled system, here Ged(s), determines which of kv k.,, h, need to be nonzero, and what their magnitudes should be for good performance. Integral control has the char­acteristic of a memory, and steady-state errors cannot persist when it is present. Rate control has the characteristic of anticipating the future values of the error and thus generates lead in the control actuation. It turns out
that all we need here is proportional control, so we choose Gp(s) = K, a constant, and the characteristic equation is

D{s) + KN^s) = 0 (11.2,5)

To proceed further, we need explicit expressions for and D. We saw in Sec. 10.2 that the phugoid approximation to Ged is quite good up to elevator frequencies near that of the short-period mode. Since we may expect that the elevator frequency needed to suppress the phugoid is of the same order as the control-fixed phugoid frequency, we may use (10.2,156) in this analysis (and this is verified a posteriori). We therefore have

Nfls) = n2s2 + ще + щ D{s) = c2s2 + crs + c0

Approximate expressions, good enough for this example, are obtained from (10.2,156) by neglecting CLg and assuming CTp = —20^ and G D^<< CL^. We then get

2 Ста

C*

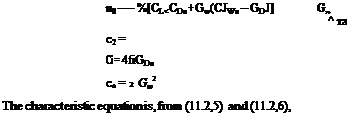XG

(c2 – f – Kn2)s2 – f- (cx + Kn, y)s — (c0 + Kn0) — 0

and the feedback is seen to affect every term in the equation. We also observe that the numerator of the open-loop transfer function Ges plays a decisive role in determining the characteristics of the closed-loop system.

The frequency and damping of the system are now obtained from (11.2,9)

/clt + KnSA ю /1 + Knjc^

c2 + KnJ ”1 + Kn2jcJ

_____ C + Knx_________ ________ (1 + Knjci)________

V (c2 + Kn2)(c0 + Kn0) V(1 + Kn2lc2)(l + Kn0lc„)

where o)n = (c0/c2)^ and 2 ^ = c1/Vc2c0 are the fixed-control phugoid parameters. Using the data for the jet transport cruising at 30,000 ft altitude given in Sec. 9.1, and Cmg = Cm^ we get the numerical values

(11.2,11)

Even with small gain К the damping of the phugoid is very much increased. The original value was £ = .0535, so to produce a dead-beat transient for which £ = 1, we require £’/£ = 18.7, which is produced by a gain —K = .17. Note that the gain is negative, since a positive error є indicates the nose is too low, and up-elevator (de < 0) is required to correct. With the gain needed for £ = 1.0, we get co’„la>n = 1.07, so the frequency has been increased by only 7%, and the phugoid approximation for Ges is clearly adequate.

This calculation shows how a human or automatic pilot could eliminate the phugoid oscillations quite simply, using readily available state information. The exact control law by which a human pilot actually achieves this result may in fact be somewhat different from that assumed here, but it is probable that в is the prime variable on which he operates.