Gortler Instability

The Gortler instability is a centrifugal instability which appears in flows over concave surfaces, but also in other concave flow situations, for instance in the stagnation region of a cylinder. It can lead to high thermal loads in striation
form, for instance at deflected control surfaces. However, striation heating can also be observed at other parts of a flight vehicle configuration [64].

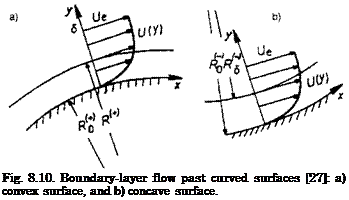
Consider the boundary-layer flow past curved surfaces in Fig. 8.10. Al­though we have boundary layers with no-slip condition at the surface, we assume that we can describe the two flow cases with the lowest-order ap­proximation

With assumed constant pressure gradient | dp/dy | and constant density, the term U2 at a location inside the boundary layer 0 < y < 5 must become larger, if we move from R to R + AR. This is the case on the convex surface, Fig. 8.10 a). It is not the case on the concave surface, Fig. 8.10 b). As a consequence in this concave case flow particles at R with velocity U attempt to exchange their location with the flow particles at the location R + AR where the velocity U — AU is present.

In this way a vortical movement inside the boundary layer can be trig­gered which leads to stationary, counter-rotating pairs of vortices, the Gortler vortices, with axes parallel to the mean flow direction. They were first de­scribed by H. Gortler [65] in the frame of the laminar-turbulent transition problem (influence of surface curvature on flow instability). Results of early experimental investigations are found in [66] and [67].

Goortler vortices can appear in almost all concave flow situations. In our context these are aerodynamic trim or control surfaces, but also inlet ramp flows [1]. They were observed in ground-facility experiments for instance at jet spoilers [68], but also behind reflections of oblique planar shock waves on flat-plate surfaces. They can appear in laminar, transitional and turbulent flow and can lead in each case to appreciable striation-wise heat loads. They
are thus not only of interest with regard to laminar-turbulent transition, but in particular also with regard to thermal loads on flight-vehicle structures.

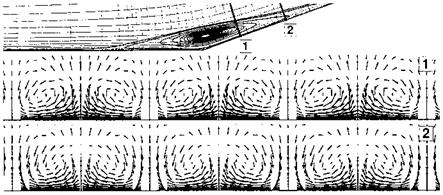
To understand the occurrence of striation-wise heat loads consider Fig. 8.11 with three vortex pairs each at the two stations 1 and 2. Shown is the perturbation flow in two cross-sections of the time-averaged re-circulation region of the ramp flow indicated at the top of the figure. The in this case turbulent flow computation was made with the DLR-CEVCATS-N RANS method [69]. The vortices were triggered, like in a related experiment, with artificial surface distortions (turbulators). They appear already in the recir­culation regime and extend far downstream behind it.

We see in Fig. 8.11 the cross-flow velocity components—the stream-wise velocity components lie normal to them. Between the vortex pairs the flow is directed towards the ramp surface and inside the vortex pairs away from it. Consequently on the ramp surface attachment lines with diverging flow patterns are present between the vortex pairs, like shown in Fig. 3.5, and detachment lines with converging flow patterns inside the vortex pairs, like shown in Fig. 3.6.

Following the discussion in Sub-Section 3.2.4, we conclude that on the surface between the vortex pairs heat fluxes—or temperatures in the case of radiation cooling—will be found which can be substantially larger (hot-spot situation) than those found inside the vortex pairs (cold-spot situation), but also in the absence of such vortices. In [70] computed span-wise heat-flux variations of ± 20 per cent for the X-38 body flap are reported.[139]

Such hot/cold-spot situations in streak form are indeed found also in laminar/transitional flow on flat plate/ramp configurations, see, e. g., [71,

72]. There a strong influence of the leading edge of the ramp configuration (entropy-layer effect?) on the ensuing Gortler flow is reported. Results from a numerical/experimental study of the flow past the X-38 configuration with Gortler flow on the extended body flaps are given in [73], see also [70].

The Gortler instability can be treated in the frame of linear stability theory, see, e. g., [14, 15]. The Gortler parameter G£ reads

where t is a characteristic length, for instance the displacement thickness Si of the mean flow.

A modification of this parameter for supersonic and hypersonic flows is proposed in [74]. It seems to be an open question whether Gortler instability acts as an operation modifier on the linear amplification process in the sense of Morkovin, [12], or whether it can also lead directly to transition (streak breakdown?). For an overview see, e. g., [75]. In [11] it is mentioned that transition was found (in experiments) to occur for G£ = 6 to 10.