Group Velocity for Finite Difference Schemes

Suppose ю = o(a, в) is the dispersion relation for a certain wave mode in two dimensions, then, as discussed in Section 4.6, the group velocity is

do do v = — e + e

Vgroup da ex + дв ey’

where ex and ey are the unit vectors in the x and y directions. For instance, the dispersion relation for both the entropy and the vorticity wave is Eq. (5.13),

ш = u0a, (5.47)

so that

дш дш

—— = u0, — = 0.

да дв

Hence,

vgroup = u0e. (5.48)

That is, the wave is convected downstream at the speed of the mean flow.

The dispersion relations for acoustic waves in a uniform mean flow are given by Eq. (5.17) as follows:

ш = u0a ± a0 {а2 + в2)1/2. (5.49)

The group velocity is

For waves propagating in the x direction, в is equal to zero. For these waves,

vgroup = u0 ± a0.

Now, for the DRP scheme, the dispersion relation of the corresponding wave is given by

ш(ш) = ш{а{а), в(в)).

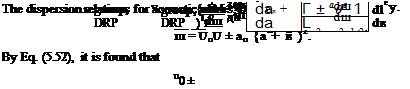By implicit differentiation, the group velocity of the wave is

For waves propagating in the x direction alone with в = в = 0, the group velocity is

For small At, йю/й<ш ~ 1. In this case, the group velocity is proportional to dа/dа. It is interesting to point out that for grid-to-grid oscillations (i. e., short waves with а Ax ~ n) dа/dа ~ -2.3 from Figure 2.4. Thus, the grid-to-grid oscillations
propagate at 2.3 times the speed of sound. The waves travel supersonically in the opposite direction.