INERTIAL COUPLING IN RAPID MANEUVERS

There is a class of problems, all generically connected, known by names such as roll resonance, spin-yaw coupling, inertia coupling, etc. (refs. 10.1 to 10.9). These have to do with large-angle motions or even violent instabilities that can occur on missiles, launch vehicles, reentry vehicles, and aircraft performing rapid rolling maneuvers. The common feature of all these is that the vehicles tend to be slender, and that rapid rolhng is present. In some of the situations that have occurred in practice, complicated nonlinear aerodynamics, and mass and configurational asymmetries have been im­portant factors in determining the motion. This subject as a whole is too large for anything approaching a comprehensive treatment to be given here. However, we present some analysis that reveals some of the underlying principles, and by way of an example show what can happen in rapid rolling maneuvers of aircraft.

Let us begin by examining a very simple hypothetical case. The body in question is axisymmetric with ly > 4- Its reference flight condition is one of constant V and o>, both these vectors lying on the axis of symmetry, the x axis. We neglect gravity entirely, and study small perturbations around the reference state. The perturbations are further constrained not to include either V or the roll rate, which remain constant at Ve and p0, respectively. We further assume that the only aerodynamic effects are pitching and yawing moments given by

— Cma<X + Gm,/i

@n = + Gnr

Because of the axisymmetry, Cn/) = — 6’r% and СПг = Ст>. Since the essence of this problem is nonlinear inertia couphng between the longitudinal and lateral degrees of freedom, we require the general equations (5.13,8) to (5.13,12) for the formulation. In applying the equations we take both the reference
lengths Ъ and c to be equal to a reference diameter d, so that A = 1. There are then four variables left in the problem, [a, fj, p, r], so we need four equations of motion. These are provided by (5.13,96 and c) and (5.13,11a and 6). In using the latter two we note that (5.13,86 and c) show that qw and rw are zero by virtue of the neglect of gravity and aerodynamic forces. (Since the net force is zero, V is a constant vector, and the wind axes have motion of translation only.) The pertinent equations are then, on making due allowance for the axisymmetry,

Gm = iyDq – (Іу – Ijfpo

Gn = KDr + (K – ^ (10.7,2)

Da. = q — Po cos «tan P — r sin a tan ft Dfi = p0 sin a — r cos a

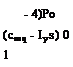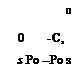On combining (10.7,1) with (10.7,2) and performing the usual linearization, the result is (using Laplace transforms of the equations)

Now we recognize that we are dealing here with the problem of gyrostability. At very large roll rates, we expect the body to display typical gyroscopic motions that will depend mainly on the signs and magnitudes of Cmx and. At vanishingly small roll rates, the equations decouple into conventional lateral and longitudinal sets, in which the sign of Gm (i. e. of the pitch stiffness) is a dominant consideration—for Gm and G both <0, a stable system is assured. We know that even if Gm^ > 0, gyroscopic stability (in the sense that motions are bounded) is achieved at large enough spin rates. This is in fact the method of stabilizing rifle bullets and artillery shells. It is therefore intuitively evident that there must be a critical roll rate for the case Gm > 0 above which the vehicle is stable—just like the critical spin rate for a common top. On the other hand there is no such intuitive notion about the case when Gma < 0, i. e. when the system is already stable at zero spin—the common case in aerospace (as opposed to balUstic) applications.

To study the stability we need the characteristic equation of (10.7,3), which is of fourth order

C4S4 + C3.S’3 + c,,s3 + crs + C0 = 0

where c4 = Iy2

сз =

c2 = -2iyGma + p04v2 + Cm* + (Іу – ixf$* (10.7,4)

C1 = %Qmapmv ~ %!Po2@m/y

c0 = [(iy-IxW + CmJ + Cm*

Unfortunately, even with all the simplifications already made, this equation is still rather too complicated to permit us to say anything simple about the roots. We therefore make a further simplification, and take Gm<[ = 0. We then have

= ї:

c3 = 0

C2 = рЛІ/ + (Іу – Ifl – 2ifim.

c4 = 0

whence Xі = ~c2 ± Vc22 – (1.0.7,5)

2c4