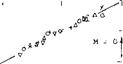Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
INFLUENCE OF COMPRESSIBILITY ON SWEPT
2. The second version has the advantage that the effective WINGS. angle of sweep (equation 29) does not have to be com
puted.
When used in subsonic airplanes, the critical Mach number of swept wings is of primary interest. However, as in other wings, compressibility also affects the aerodynamic forces at speeds below the critical.
ANGLE OF SWEEP. As in incompressible flow, the lift of a swept wing is approximated by that of the two panels, say at Уг of their span, exposed to the components of the air speed each normal to their quarter-chord or equal – pressure axes; that is to (V cos/) as in figure 2. However, as pointed out in (21,b, c) the Prandtl-Glauert rule (see Chapter VII) can also be formulated as saying that any wing in compressible fluid flow produces the same lift as a wing whose dimensions in the direction of flow have been increased in proportion to the Prandtl factor P = 1/ /1 — M*. This means that not only the chord, but also the angle of sweep of that reference wing are increased. Accordingly, the effective angle (subscript e) corresponds to
tan j^= tan _Л+/ Гі — M2 (29)
It then follows that
cos 7еУі — (M cos – cos Ар/ 1-М2 (30)
where У1 — M2 as in Chapter VII.
LIFT ANGLE. Based upon the foregoing and equation (21) the lift-curve slope of a swept wing with infinite aspect ratio, in a compressible fluid flow, is expected to be
Assuming now that the induced drag and the angle due to lift (20/A) are no larger than in straight wings, the lift angle of swept wings with higher aspect ratios (say above A = 4) is
d<X° IdCL = (10 /l – (M cos A+f /cos – Л+) + (20/.A)
(33)
where (M cos Л*) can be considered to be an effective Mach number, for which the root in the equation can be taken from figure 1 in Chapter VII. Available experimental data are plotted in figure 22. While evaluating the many sources as in (22), it was found that on the average, wings tested in combination with a fuselage have doL /dCL values larger by 1° , and half-span wing models (mounted on the wind-tunnel wall) have values lower by
о о
1 , than plain 45 swept wings. However, results obtained on half wings, placed on so-called bumps in wind tunnels or on the wings of flying airplanes as in (22,c, h) for example are not affected by the thin boundary layer developing over those bumps. To obtain one single line, 20/A = 5° plus/minus 1 was subtracted from the reported lift angles; and the parameter of the section, expected to be
(do/ /dCL) cos – Л+= 10° й – (M cos Л)2 (34) was plotted accordingly, figure 22, with promising results.
о 65A006 W’BODY (22,a)
/ W1 BODY ON STING (22,b)
+ 1/2 SPAN ON BUMP (22, c)
о Rc = 3(10)6, ВОШ(22, d) x 65A006 W1 BODY (2 2,e) ф W1 TRIMMED H’TAIL(22,f)
V DITTO, ccs/A= 0.8 (22 , g) о HALF-SPAN MODEL (22,d)
— HALF WING(BUMP) (22,h)
|
dCL/doc°2 =0.1 cos Л//1-М2) dCL /doc°2 = 0.1 cos – Л I Vl — (M cos – Л+)г (31) where 0.1 = (dCL jdoC° ) of a straight wing, with subscript 2 indicating two-dimensional conditions of flow. The lift angle is accordingly: do /dCL= 10/1 – Мг /cosAc= 10/ГАМ cos A)* /cos A. (32) |
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
(21) Principles and rules for compressible flow:
a) Liepmann, “Elements Gasdynamics”. Wiley 1957.
b) Diederich, Correlation, NACA TN 2335, as (1 l, a).
c) Goethert, Bodies, Ybk D Lu 1941; NACA TM 1105
d) Kuchemann, Bodies of Revolution, J Aeron Sci;
Cp/Cp, nc = AV/V = ‘Fr = 1/(1 – мг A
Figure 22. Sectional component of the “lift angle” of 45° swept wings, with A = 4, as a function of the Mach number parameter.
(22) 45° swept wings as a function of Mach number:
a) Polhamus, Directional Stability, NACA TN 3896.
b) Donlan, Testing Techniques, NACA RM L1950H02.
c) Polhamus, Wings on Bump, NACA RM L51C26.
