NUMERICAL EXAMPLE—PITCH/ROLL COUPLING OF A SMALL AIRPLANE

To show how the nonlinear inertia terms can affect the motion of an airplane we consider a small maneuverable single-engined jet airplane. Its principal characteristics are

W = 6000 lb, 8 = 216 ft2, A = 6.0 b = 36.0 ft, c = 6.0 ft 4 = .170 x 104 slug ft2 4 = .120 X 105 slug ft2, Izx = o 4 = .140 X 105 slug ft2

Note that Ixjlz is only.121, as compared with about.4 for the transport airplane. The pertinent aerodynamic data for flight at 500 fps at sea level are given as

	= -.081,		= 4.35, CL&	О II 11
	= -.435,	Сщ*	= ~2-1.	= -9.73 r
	= -.081,		= -.442, Clr	= .0309
%	= .0218,		= 0, cnr = –	.0424
	= 0. omi	e	-1.07, 0цш =	-24> 0^
CT	= —/ЗС4,	Or.	= — AglCt, w 1 *9	GT = .017

The value of pcrit calculated from (10.7,9) is.0796. In applying the general nonlinear equations, we assume that Да, /?, remain small, that linearization is permissible with respect to them, and that the speed is constant.

With these assumptions, (5.13,8) et seq. yield the following system of equations.

СтР Cc d~ ^os <i3w — %рА. Гц7

—Д а ■ -f ®^s ^iv cos 4>w ~ 2////jj-

Ci = Кащ ~{j2- K^yr Cm = IvDq A(iz – ijrp Cn = izDf – (ліх –

A

Da = q — qw — ^

Л£ = !> + 1 Да – – J. 4 J.

DJ>W = ^ ^ _|_ g tan sin ^^7 H “ tan 6ц? cos фуу A A

D0jj7 = cos ~

Pw = P + + Да f

= CcpP

@L — C L. fJ-

Ci = Olf(} + Сгр + Огг + GUa Sa Cm Cmf^ + Cm, jDa Cm g ~b Cm/jede

Cn = Cnp + CnJ> + Gnf

The logical structure of these is essentially as in Fig. 5.6.

The above equations were programmed for solution on a digital computer,

using a Runge-Kutta algorithm for solving differential equations. Solutions were obtained for two different sets of conditions:

(i) Initial condition of rolling at rate p{, with all other initial values zero, with |(3e| at 2°, and with da set at the value required to make pss = pi [see (10.6,8)]. Thus the initial value of p would be zero, producing a condition somewhat like that of Phillip’s analysis.

(ii) All initial values zero, with a pitch maneuver initiated by elevator elevator deflection at t = 0 and a subsequent roll maneuver super­imposed by a step change in Sa.

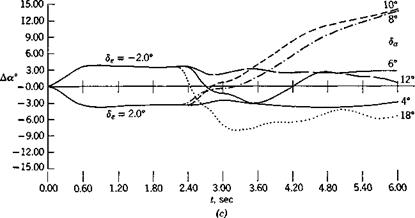
Figure 10.18 shows the angle of attack variation in the first case, (a) for pitch-up and (b) for pitch-down. A striking result is the difference between positive and negative elevator angle, a difference that results entirely from the nonlinearity of the equations. Even for very large aileron angles, there is no evidence in (a) of instability, and only for the case of |<5J = 14.7° does Да become momentarily excessive. On the other hand case (b) develop excessive Да quite suddenly when [da| goes from 4.2 to 6.3°. The difference in behavior in these two cases is largely attributable to the difference in the roll-rate time histories, which in turn results from the fact that /5 > 0 in (a) and (3 < 0 in (6). (The roll rate results are not presented on the figures. The following comments are based on the computer output.) In the case p{ = .060, de = 2.0°, p first decreases slightly, then increases with time as a result of rolling moment due to side-slip, crossing over the critical value.0796 at about.8 sec, and remaining larger till the end of the calculation. Very soon after p exceeds pcrit, Да starts to increase rapidly. On the other hand, for pt = .040, p never reaches the critical value, and Да is “well-behaved.” In Fig. 10.18a, p{ — .140, the rolling moment due to sideslip is negative and decreases the roll rate so that it falls below the critical value at t = 2.6 sec. This is again compatible with the reduction in Да that occurs at about the same time. It appears that the critical roll rate derived by Phillips is a very useful criterion for a “well-behaved” transient.

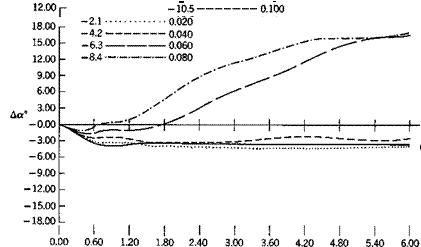
Figure 10.19 shows the variation of Да for the second case, which is a realistic maneuver, resulting after 5 sec in a pitch-up (or down) of about 20°, and a roll when da = 8° of about 1-]- revolutions. Again the lack of symmetry between pitch-up and pitch-down is clear, the latter being the unfavorable case for a roll to the left. The difference between Да for 8a = 4° and 6a = 8° or 10° is striking. In the former case the detailed solution shows p < pcrit for the whole time, whereas the latter two have p > pcrit almost from the onset of the rolling motion. For the pitch-up case as well, peHt is exceeded for 8a= 12° and 18°, but not for Sa = 6°.

Fro. 10.18 Variation of Да during rapid roll, (a) Pitch-up case, 8e = down case, 8, = 2.0°.

In the discussion of these examples we have studiously avoided the use of the word “stability” in describing the solutions, using “well-behaved” instead to denote “acceptable behaviour.” We have not in fact discovered anything about the stability of the solution presented, in the strict Lyapunov sense. They may or may not be continuous functions of the initial conditions as t —> со, (although they certainly appear to be continuous for the range of

Fig. 10.19 Variation of angle of attack in a combined pitch/roll maneuver.

t considered). Furthermore, the stability in that sense is actually irrelevant (see closing remarks of Sec. 3.5). Whether or not the maneuver is an accept­able one is governed entirely by the size of the Ax and Д/3 excursions that can be tolerated without structural failure or loss of control and not by the theoretical stability of the solution.