Profile drag relations

The profile drag (5.32) can be rewritten as

Dp = Ц pu (VA – u) dS

5.6.1

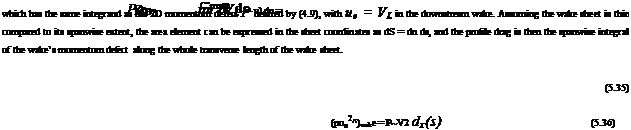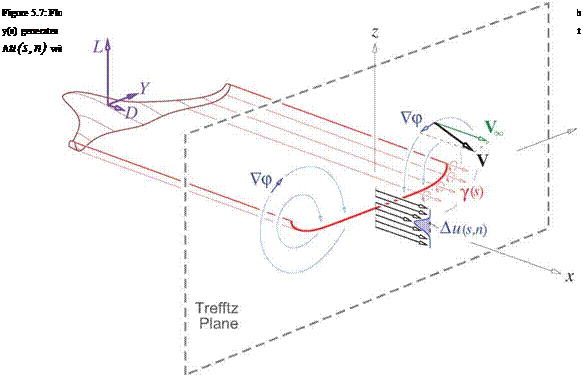
Trefftz-plane velocities

As stated earlier, the perturbation potential velocity Vp is associated with the wake vortex sheet strength 7 = y X. Based on the equivalence between vortex and doublet sheets presented in Section 2.5, this 7(s) is related to the sheet’s potential jump Ap(s) as follows.

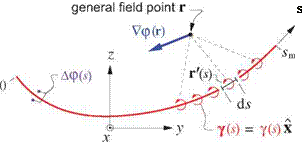
Referring to Figure 5.8, this vortex sheet defines the 2D perturbation velocity field Vp in the Trefftz plane, via the usual 2D superposition integral,

where r is the yz field point, and r'(s) = y'(s) y + z'(s) Z parametrically defines the shape of the sheet.

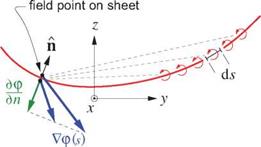
Figure 5.8: Vortex sheet in Trefftz plane, with associated perturbation velocity field Vp, which has normal velocity component dp/dn on the sheet itself.

For the particular field point locations on the sheet itself, we can also define the normal component of this velocity.

One of the two velocities (or their average) on either side of the sheet can be used here, since they have the same normal component, which is continuous across any vortex sheet.

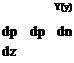Many applications consider the simpler situation of a flat wing of span b, where the vortex sheet is also flat and lies on the y axis from —b/2 to b/2. The above relations then simplify as follows.

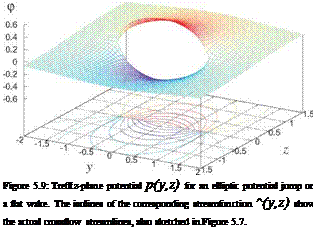
The potential field p(y, z) for this flat-wake case, with an elliptic potential jump Ap = /l — (2y/b)2, is shown in Figure 5.9. The corresponding streamfunction shows the crossflow streamlines.