Solution of the boundary-layer equations for a flat plate

There are a few special exact solutions of the boundary-layer equations (7.7) and

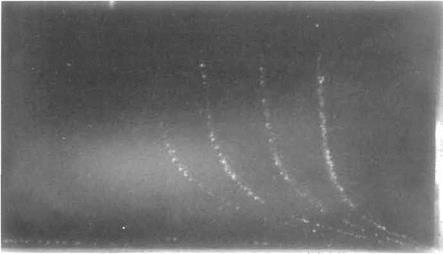
(7.14) . The one for the boundary layer in the vicinity of a stagnation point is an exact solution of the Navier-Stokes equations and was described in Section 2.10.3. In this case, we saw that an exact solution was interpreted as meaning that the governing equations are reduced to one or more ordinary differential equations. This same interpretation carries over to the boundary-layer equations. The most famous, and probably most useful, example is the solution for the boundary layer over a flat plate (see Fig. 7.7). This was first derived by one of Prandd’s PhD students, Blasius, in 1908.

A useful starting point is to introduce the stream function, ф, (see Section 2.5 and Eqns 2.56a, b) such that

This automatically satisfies Eqn (7.7), reducing the boundary-layer equations to a single equation (7.14) that takes the form:

дф д2ф сРф 1 djр д3ф

ду дхду дх ду2 р dx V ду3

For the flat plate dp/dx = 0.

Consider the hypothetical case of an infinitely long flat plate. For practical appli­cation we can always assume that the boundary layer at a point x = L, say, on an infinitely long plate is identical to that at the trailing edge of a flat plate of length L. But, if the hypothetical plate is infinitely long, we cannot use its length as a reference dimension. In fact, the only length dimension available is v/lloo. This strongly suggests that the boundary layer at a point xi, say, will be identical to that at another point *2, except that the boundary-layer thicknesses will differ. Accordingly we

propose that, as suggested in Fig. 7.7, the velocity profile does not change shape as the boundary layer develops along the plate. That is, we can write

We now tranform the independent variables

so that

Ш,

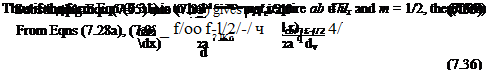=i

Likewise, if we replace ф by дф/ду in Eqn (7.33) and make use of Eqn (7.36), we obtain

сРф

дхду

Similarly using Eqn (7.34) and (7.36)

^Ф_д_(9ф_д_(и V=^-l/2u dV

ду2 дуду) dy 00 dr,) ^ 00 drj2

дуъ «« и«>^

We now substitute Eqns (7.36)-{7.40) into Eqn (7.29) to obtain

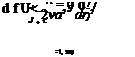Then cancelling common factors and rearranging leads to

As suggested, if we wish to obtain the simplest universal (i. e. independent of the values of Uoo and v) form of Eqn (7.41), we should set

Uaо….

2ua2

So that Eqn (7.41) reduces to

^+/^ = 0- dr^ drj2 ’

The boundary conditions (7.15) become

Л

drj

The ordinary differential equation can be solved numerically for /. The velocity profile d//d?7 thus obtained is plotted in Fig. 7.10 (see also Fig. 7.11).

From this solution the various boundary-layer thicknesses given in Section 7.3.2 can be obtained by evaluating the integrals numerically in the forms:

1.7208

Momentum thickness Energy thickness

°=ГН’-й>=&Ш’ – (I) V ‘W£ ™

The local wall shear stress and hence the skin-friction drag can also be calculated readily from function f(rf):

fdu drj (du

_ TJ ux(d2f ux

— ( j 7 I 0.332fJiUoQl

V 2vx drf)^ V их

4—– v—– ‘

0.332V7

Fig. 7.11 Velocity profile in a boundary layer: The velocity profile that forms in a boundary layer along a flat wall is made visible by lines of aluminium powder dropped from a trough on to the flowing fluid surface. The fluid is a dilute solution of wallpaper paste in water. The Reynolds number based on distance along the wall is about 50000. See also Fig. 7.3 on page 376. (The photograph was taken by D. J. Buckingham at the School of Engineering, University of Exeter, UK.)

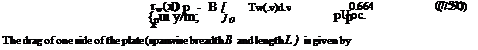Thus the skin-friction coefficient is given by

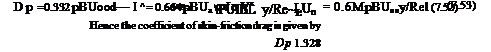
Thus combining Eqns (7.49) and (7.51) we find that the drag of one side of the plate is given by

Example 7.2 The Blasius solution for the laminar boundary layer over a flat plate will be used to estimate the boundary-layer thickness and skin-friction drag for the miniature wing of Example 7.1.

The Reynolds number based on length Лгу, = 2000, so according to Eqns (7.45) and (7.46) the boundary-layer thicknesses at the trailing edge are given by

1 7208 6* = —^— x 0.67 = 0.23 mm

5

Remembering that the wing has two sides, an estimate for its skin-friction drag is given by

1 і 1.328 j

Df = 2 x CCF x – t/2.SZ, = . x 1.2 x 52

г иг ~ aa /onnn