Steady Transonic Flow, Non Linear Approach
Equation 2.15 is the non linear equation which is satisfied by the velocity potential. If we omit the time dependent terms of Eq. 2.15, we obtain the following non linear equation for the velocity potential in two dimensional steady flows
(d2 — ФІ )/xx +(a2 — /2 )/yy — 2/x Фу /xy = 0 (6.26)
Here, a denotes the local speed of sound and the subscripts denote the partial differentiation with respect to x or y. The character of Eq. 6.26 changes depending
on the speed of sound in a transonic flow. If speed of sound is higher than the local flow speed, then the equation is elliptic, and it becomes hyperbolic if the flow speed exceeds the speed of sound. For this reason, the solution of Eq. 2.26 can be obtained either with specific analytical methods for specific profile shapes or numerical methods for arbitrarily shaped airfoils. In general, for a profile with a thickness immersed in a high subsonic free stream the flow speed increases due to thickness effects until reaching the sound line where the flow speed is equal to local speed of sound. After maximum thickness, the supersonic flow expands and speeds up while its pressure drops down. Before reaching the trailing edge there is a sudden increase in the pressure so that the flow pressure eventually reaches the wake pressure. This sudden pressure increase is a normal shock, which is in harmony with the physics of the flow for transition from supersonic to subsonic flow regime. However, for very special geometries it is possible to have shockless transonic flow via inverse design (Nieuwland and Spee 1968). First shockless transonic flow was studied for symmetrical quasi elliptical profiles (Baurdoux and Boerstoel 1968), and thereafter these techniques were developed for non symmetrical airfoils called supercritical airfoils (Whitcomb 1956; Bauer et al. 1972, 1975).
Now, as an example to the shockless transonic external flow we can obtain the surface pressure coefficient of the symmetrical quasi elliptical profile with finite element solution of Eq. 6.26. Since Eq. 6.26 is a nonlinear equation we have to solve it with an iterative technique. In addition, it has an elliptic – hyperbolic character; therefore, the information in the elliptic region must be carried in all directions. However, in the hyperbolic region the information must travel only in downstream of the node concerned. This forces us to use artificial viscosity with a proper control system while forming the coefficient matrix. This means for the elements in the supersonic region only the information travelling in downstream is permitted, otherwise it is eliminated. This approach gives us a convergent iterative scheme for the solution of the velocity potential (Ecer et al.
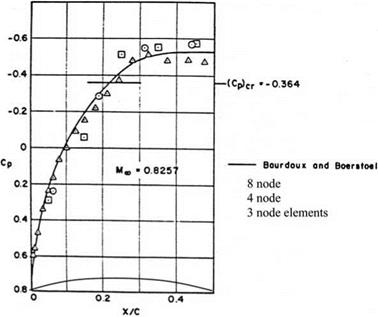
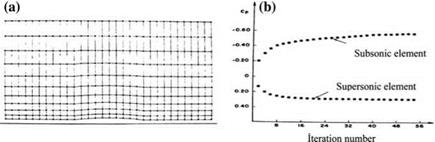
1977) . In Fig. 6.3 the finite element results with quadrilaterals are compared with the analytical solution for the surface pressure variation Cp of a quasi elliptical Nieuwland profile. Although, a course grid is used, 31 x 11, in computations a good agreement with the analytical solution is achieved in subsonic region and a satisfactory agreement is observed after the critical pressure where local Mach number exceeds unity. Shown in Fig. 6.4a is the discretized flow field for the finite element solution. The 50 step iteration convergence history of the subsonic and the supersonic surface pressure values are given in Fig. 6.4b.
The same elliptic-hyperbolic mixed problem was also solved by Murman and Cole using finite difference method with much finer grid on the surface of the airfoil. Their solution agrees well with the analytical solution since they use 50 points on the surface to increase the accuracy. However, their solution required more CPU time. Murman and Cole also considered the off-design behavior of the profile by giving solutions obtained for the free stream Mach numbers slightly different from the design Mach number.
|
Fig. 6.3 Surface pressure distribution for 10.76% thick Nieuwland profile at M = 0.8257 |
The purpose behind analyzing the transonic flows in detail lies in designing new profiles either without shock or with very weak shock at high subsonic Mach numbers. It is a well known fact that if there is a shock on the surface of the profile at subsonic free stream Mach numbers, the drag coefficient becomes the double of the shockless case. The cause of this drag rise is the shock induced boundary layer separation and the entropy rise across the shock. On the other hand, if the shock occurrence on the airfoil surface is delayed with the increasing of the free stream Mach number, then the lift coefficient will rise while the drag coefficient almost remains the same. Now, we can compare qualitatively the upper and lower surface
|
Fig. 6.4 For the symmetrical quasi elliptical airfoil, a finite element grid, b convergence |
![]()
 |
|
 |
|
(b) M„ = 0.80
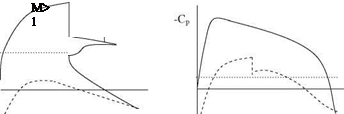
Fig. 6.5 Transonic flow, a conventional profile, strong shock, b supercritical profile, weak shock
pressure coefficients and sonic lines for the conventional and supercritical profiles in Fig. 6.5.
As seen in Fig. 6.5a, there is a strong shock present at the upper surface of the conventional airfoil to cause a boundary layer separation whereas at a considerable higher free stream Mach number the supercritical airfoil has weak shocks at the lower and upper surfaces without any flow separation. In conventional airfoils the critical Mach number is reached for lower free stream speeds with lift loss and drag increase as opposed to the supercritical airfoils for which the critical Mach number and the lift is higher and the drag is lower. As an example for a classical NACA airfoil when the free stream Mach number is increased from 0.65 to 0.69 the drag coefficient increases 50%. For a supercritical airfoil, on the other hand, the drag coefficient increases only 10% for the Mach number increase from 0.65 to 0.79 and for M = 0.80 it goes back to the value that was attained at M = 0.65 (Whitcomb and Clark 1965). However, if the free stream speed exceeds the design value of 0.80, the drag coefficient shows a sudden increase. This means one should expect poor performance from the supercritical profiles at off design conditions.