Strouhal-Number Versus Helmholtz-Number Scaling
For self-similar flows the properties of which do not essentially vary with the Reynolds number, the amplitude and the frequencies of velocity fluctuations are both proportional to the mean flow speed. The spectral shape of the far-field sound extends wider for higher speeds, with increased levels. The flow statistics involved in the forcing source terms is expected to scale according to the Strouhal number St = fc/U0. As a result, plotting the reduced PSD Spp U0 (n 1) as a function of the Strouhal number and ignoring non-compactness interferences must produce a perfect collapse of the curves, if the overall (frequency-integrated) acoustic intensity scales like Un. This property should be used systematically to scale broadband noise data in aeroacoustics. In the same time higher frequencies triggered by higher flow speeds make the airfoil chord less compact, and departure from the selfsimilarity is expected in the sound signature from the onset of interference fringes. Apart from this, any geometrical environment of a flow is characterized by resonant frequencies which do not essentially depend on flow speed. It can be guessed that resonance and interference features, in particular related to chord-wise non-compactness, rather depend on the Helmholtz number He = kc. Indeed plotting the PSD as a function of frequency or
Helmholtz number preserves the non-compactness dips and humps at the same places but cannot produce a collapse over the entire frequency range. Plotting as a function of the Strouhal number provides a better overall collapse except that the dips are now at different Strouhal numbers for different speeds. Yet the Strouhal-number scaling is more physically consistent when tracking scaling laws of sound-generating mechanisms.
|
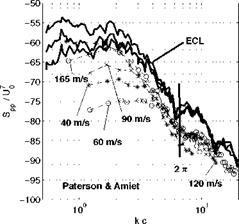
Figure 21. Helmholtz-number scaling of turbulence-airfoil interaction noise. Symbols stand for the NACA-0012 of Paterson & Amiet (1976) and thick lines for the thin cambered airfoil tested at ECL. Grid-generated turbulence, observer at 90° in the mid-span plane. |
The sample results collected in Fig. 21 are taken again from Paterson & Amiet (1976) and the ECL data for a thin cambered airfoil (Figs. 18 and 19). A good collapse is achieved by plotting Spp/U0 as a function of the Helmholtz number kc, if the plot is aimed at emphasizing the humps and the dips attributed to non-compactness. Yet unacceptable scatter is found at lower frequencies. The first dip occurs quite close to the value kc = 2 n for which the acoustic wavelength is equal to the chord length, which is somewhat expected for an observer at 90° . The slight frequency shift of the dip between both sets of data is attributed to the different geometrical design. The sound levels also differ because of different experimental conditions and because of the thickness effect of the NACA-0012. This simple example illustrates that aerodynamic noise in the presence of solid surfaces combines intricate flow and geometry effects. The duality He-versus-St has been identified in many applications, for instance by Neise & Barsikow (1982) who discussed the acoustic similarity laws of low-speed fans.