Thrust and Drag

It has already been stated that in the two-dimensional case the jet is ultimately turned in the direction of the free stream and that the thrust is equal to the flux of momentum in the jet. In the actual case the thrust will be something less than the flux of momentum due to frictional losses on the boundaries of the jet in contact with the solid surfaces of the airfoil or with the slowly moving free-stream air.

For a finite, jet-flapped wing the jet is ultimately deflected in a direction slightly different from the free-stream direction because of the downwash.

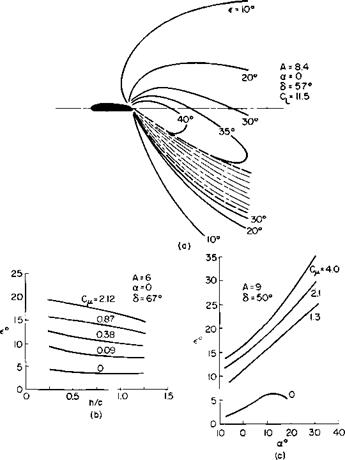
Fig. 7-11. Experimental measurements of downwash behind jet-flapped wings: (a) contours of constant downwash angle; (b) variation of downwash with tailplane height; (c) variation of downwash with incidence.

This results in a reduction in the thrust which can be viewed as an addition to the induced drag.

If au denotes the downwash angle at infinity by the application of the momentum theorem far ahead and behind the wing, the thrust and lift become

T =	– у)иА +	jj (P ~ Pco) dy dz,	(7-27)
L =	«i. ftijVj + pVAj	w dy dz.	(7-28)

These integrals are evaluated over the whole yz-plane at infinity, that is, the

Implicit in the derivation of (7-31) are the assumptions of an elliptical distribution of both Г and and the assumption that the downwash angle is small. The last can be checked with Eq. (7-30). Should a, prove large, then (7-31) must be multiplied by the factor obtained from Fig. 3-9, using an effective aspect ratio A’ defined by

A’ = A + (7-32)

71

This is still only an approximate correction, for the momentum and vor – ticity in the jet were neglected in arriving at Fig. 3-9.

The net thrust coefficient for a finite wing with full-span jet flaps can now be written as

Г2

г = r – L T M nA + 2CM

Reference 4 suggests modifying this equation in the following way:

CDo is the profile drag at zero lift without blowing, whereas r and к are correction factors for the theoretical values of the thrust and induced drag,

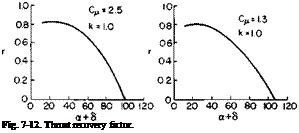
respectively. The values of r and k, given in Ref. 4, depart appreciably from unity, and we wonder whether this departure may not be the result of neglecting the deflection of the trailing vortex sheet in developing (7-31) rather than of a severe loss of jet thrust. For values of a + S below 40° r is approximately 0.8, which seems reasonable. Above 40°, however, r falls off

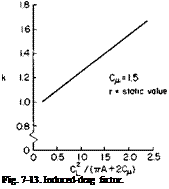
rapidly to zero at about an angle of 100°. The factor k, however, according to Ref. 4, increases nearly linearly with СЦ(пА + 2CM) from к = 0.95 at zero to about 1.55 at C]J(nA + 2CM) equal to 2.0. This is considerably less for к than Fig. 3-9 would indicate. Hence some of the rapid decrease of r with a + <5 beyond 40° may be caused by an incorrect assessment of the factor к in reducing the data.

This general area is an uncertain one at the present time and is in need of further study. However, since they are based on experimental data, and in the absence of another method, values of r and к taken from Ref. 4 are presented in Figs. 7-12 and 7-13.

Ground Effect

The effect of the ground on a jet-flapped airfoil is similar to conventional airfoils if the momentum coefficient is not too great. If CM is high enough, the jet can impinge on the ground and effectively blocks the flow between the lower surface of the airfoil and the ground. With increasing or 8 a vortex forms below the airfoil and reduces the pressure on the rear lower

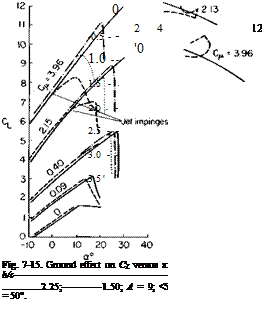
Fig. 7-14. Ground effect on C, versus С/х.

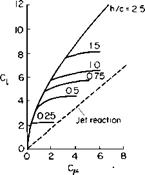
surface. Further increases in Сд lead to little or no change in C, but to a rapid forward movement of the center of pressure. Lift data on a two – dimensional section at a = 0° and 8 = 58° are presented in Fig. 7-14 for various height-to-chord ratios. Below h/c values of approximately 1.5, the ground is seen to have a significant limiting effect on C,.

Somewhat similar data are presented in Fig. 7-15 for a wing of aspect ratio 9. For Сд values of 0.40 or less the jet does not impinge on the ground for the lowest clearance studied of 1.5 c. Hence for these C^ values there is a slight increase in C, for an incidence angle below the stall. However, the angle of stall decreases with decreasing height and there is a slight decrease in CLmax. For a C„ of 2.15 and higher the jet impinges on the ground at the incidence angles shown; a significant decrease in CL results for angles above these critical values.

The effect of ground clearance on pitching moment and thrust is shown for the finite wing in Figs. 7-16 and 7-17. Again the effect is negligible until Сд and a are large enough to cause jet impingement. Above these values

significant changes are seen to occur in Cm and CT ; Cm becomes more positive and CT drops considerably.

Possibly the most serious ground effect, in addition to the effect on CL, is the effect on the downwash at the tail, which is shown in Fig. 7-18 for two different incidence angles for 8 = 50° for C„ from 0 to 3.96. For a of 20°, 8 — 50°, and = 3.96 the downwash angle is seen to drop from 30° out of ground effect to nearly zero at one chord length above