Trefftz Plane Integral Evaluation

5.8.1 Fourier series method for flat wake

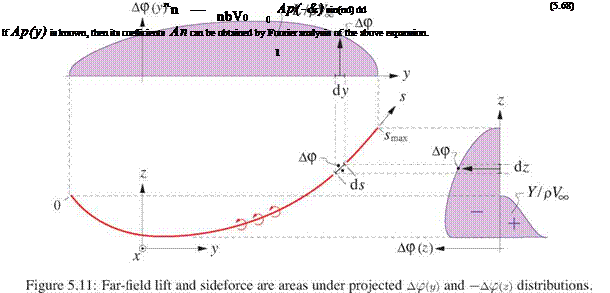
The mathematical technique used in the lifting-line wing analysis described in Appendix E also provides a convenient means of computing lift and induced drag for the flat-wake case if we make the substitution Г ^ Ap. The potential jump is first expanded as a Fourier sine series in the angle coordinate d.

The Trefftz-plane lift integral (5.65) is seen to be the same as the lifting-line result (E.19), and depends only on the first coefficient Ai.

rb/2 і

L = A<pd у =

-b/2 2

The flat-wake normal velocity dp/dz defined by (5.41) is seen to be twice the lifting-line downwash wwake definition (E.2). This is evaluated in terms of the Fourier coefficients by result (E.10).

The flat-wake induced drag integral (5.48) can now be expressed in terms of the Fourier coefficients, by the lifting-line result (E.20).

The factor 1+5 in (5.71) is sometimes replaced by the inverse of the span efficiency, 1/e.

By choosing some suitable reference area Sref, with corresponding aspect ratio AR = b2/Sref, the above lift and induced drag can be put into convenient dimensionless forms.

For a given specified lift and span, the above results show that the minimum induced drag is obtained if 5 = 0, or e = 1, or equivalently A2 = A3 … = 0, and the potential jump has an elliptical distribution on the wake. For this case the normal velocity is also constant everywhere across the wake.