Unsteady Transonic Flow, Supersonic Approach

We have demonstrated before that for the supersonic approach e0 > 0 is the restriction. If we consider simple harmonic motion, two dimensional form of Eq. 6.8, with Laplace transformation of x coordinate, becomes

ф0 — i2/0 = 0, i = eos2 + fo s — d (6-21)

Here, ю is the angular frequency, and f0 = f0 + ^—ію, d = (a/aM)2.

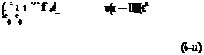The solution of Eq. 6.21 in the Laplace transformed domain can be performed similar to that of Eq. 6.8. The inverse transform gives us the solution ф0 in x coordinates together with the prescribed boundary conditions as follows

For a profile oscillating vertically with h, Eq. 6.22 becomes

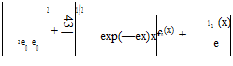
/0(z = 0) = he01/2 Here we define:

We can take the limit of Eq. 6.23 as M? = 1 to obtain the expression for the perturbation potential

Equation 6.24 is used to obtain the pressure coefficient for a simple harmonic vertical oscillation of a thin airfoil

Here, the motion is prescribed as h = heixt, and the reduced frequency is defined as k = xb/U.

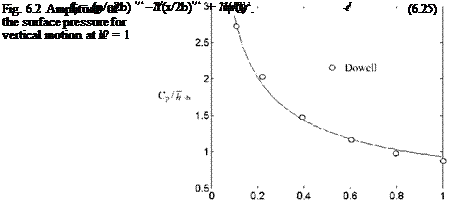
Example 6.1 Find the amplitude of the surface pressure for a profile in simple harmonic vertical oscillation at M = 1 and k = 0.25

Solution Let us take x0 = b, e0 = 0.12 and f0 = 2.4/b to find the surface pressure from Eq. 6.25. The plot of surface pressure coefficient is given in Fig. 6.2 using the complex amplitude given by 6.25. Also shown in Fig. 6.2 is the results of Stahara-Sprieter, given in Dowell, for 6% thick Guderly profile.

Comparisons of the graphs indicate that solution with 6.25 is in good agreement with the reference values.

So far we have obtained the transonic steady and unsteady solutions based on local linearization with neglecting the thickness effects. In next section we are going to see the numerical solution of nonlinear transonic flow equation with thickness effects.