Vortex-Shedding Noise Results

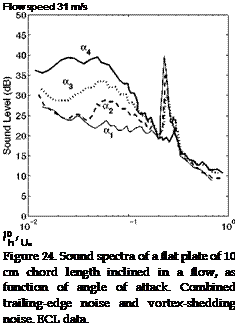
Vortex-shedding sound is a less documented topic. Indicative results and modeling attempts are mentioned in this section, for a flat plate with rectangular trailing-edge. Complementary elements are found in the book by Blake (1986). Typical far-field sound spectra are first plotted in Fig. 24 for an inclined flat plate tested in an open-jet anechoic wind tunnel. Because the flow is deflected by the mean lift acting on the plate, precise values of the geometrical angle of attack are indicative. Only the qualitative features of the flow and the related acoustic signature make sense, described here for increasing values of the angle from ai = 0 to a maximum value a4. Even higher values would correspond to stall. The relative thickness of the plate is 3%. At zero angle of attack, a large peak is heard at the expected Strouhal number of 0.2 built on the plate thickness h. As the angle increases that peak reduces whereas a wide hump grows at lower frequencies. The higher the angle of attack, the lower and wider the associated frequency range. The bump is attributed to trailing-edge noise; indeed the flow separates at the leading edge and reattaches on the suction side of the plate, triggering a turbulent boundary layer, similar to the case of the CD airfoil, Fig. 22-c. The drop of the peak is caused by a loss of coherence and a progressive deactivation of the vortex shedding by increasing upstream disturbances. The frequency shift is attributed to different local flow accelerations at dif­ferent angles of attack. It is concluded that both vortex-shedding sound and trailing-edge noise can coexist if the frequency range of the latter does not cover the one of the former. Yet competition obviously takes place.

The same plate of 3% thickness tested on a different nozzle produces the results of Fig. 25, taken from Chang et al (2006) and Roger & Moreau (2010) for illustrating the accompanying prediction methodology. In the first configuration at zero angle of attack, vortex shedding is well structured and not significantly influenced by disturbances developing upstream in the boundary layers. The associated sound can be predicted with eq. (19). The needed upwash spectrum is provided by the model calibrated in Fig. 17. The agreement is perfect in this case, dealing with the narrow-band signature only.

The procedure has been repeated for the geometrical angle of attack of 5°. In this case vortex shedding is disturbed by a higher turbulence level in the boundary layers and again the emergence of the peak is reduced as already emphasized in Fig. 24. Because of computational cost issues the nu­merical simulations ignored the flow-deflection effect in the experiment and some uncertainty results in the definition of the input data. An empirical spectral shape has been again defined anyway and the effect of the uncer­tainty assessed by the upper and lower estimates of the acoustic signature

in Fig. 25. For completeness, the trailing-edge noise prediction achieved with the model of section 5.2 fed with measured wall-pressure statistics is reported, again showing a satisfactory agreement.

The flat-plate test-case illustrates a hybrid application in which input data are partly measured and partly provided by Computational Fluid Dy­namics. The good overall agreement achieved here is in favor of the physical consistency of the reversed Sears’ problem. However the practical applica­tion is made tricky by the non-homogeneity of the velocity in the near wake.