ACCOUNTING FOR EFFECTS OF COMPRESSIBILITY AND VISCOSITY

The potential flow model presented in this chapter results in a very simple mathematical model that can be transformed into a very efficient and economical numerical solution. This resulted in the development of three – dimensional “panel codes” for arbitrary geometries and, naturally, modifica­tions were sought to improve these methods beyond the limits of incompres­sible inviscid flows. Some of these modifications are listed here.

Effects of Compressibility

The first and most straightforward modification to an incompressible potential – flow based method is to incorporate the effects of “low-speed compressibility” (e. g., for M <0.6). This can be obtained by using the Prandtl-Glauert rule, as developed in Section 4.8. Thus, small-disturbance flow is assumed, and a compressibility factor f} can be defined as

j8 = Vl – M2 (9.44)

If the free stream is parallel to the x coordinate then the x coordinate is being stretched with increased Mach number while the у and z coordinates remain unchanged. Consequently an equivalent incompressible potential ФА/=0 can be defined such that

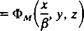(9.45)

Once the x coordinate is transformed, the equivalent incompressible potential problem is solved as described previously. This procedure results in an increase in the aerodynamic forces (as noted in Section 4.8) and

Effects of Thin Boundary Layers

When analyzing high Reynolds number flows in Section 1.8, it was assumed that the boundary layer is thin, and the boundary conditions are specified on the actual surface of the body. However, by neglecting the viscosity terms in the momentum equation, the information for calculating the viscous surface friction drag is lost too.

It is possible to account for the viscosity effects such as displacement thickness and friction drag by using a boundary-layer solution that can be matched with the potential flow solution. Two of the most common methods for combining these two solutions are as follows.

1. The first approach is to use a boundary-layer solution, usually a two – dimensional model along a streamline, which will work for simple wings and bodies. The solution begins by solving the inviscid potential flow, which results in the velocity field and the pressure distribution. This data is fed into two-dimensional boundary-layer solutions that provide the local wall friction coefficient and the boundary-layer thickness. The friction coefficient can be then integrated over the body surface for computing the friction drag. If the displacement thickness effect is sought, then a second iteration of the potential flow computation is needed, but now with modified surface geometry. This
modification can be obtained by displacing the body panels according to the local boundary-layer displacement, and the procedure can be reiterated until a satisfactory solution is obtained. Some of the principles of a computer program (e. g., the MCAIR panel code) that uses this method are presented in Ref. 9.5.

2. The second approach to incorporate boundary layer solutions into panel codes is to follow the procedure described above, but to account for the displacement effects by a modification of the boundary conditions instead of a change of the surface geometry. In this case, at each panel the normal flow is given a certain blowing value that accounts for the local boundary-layer displacement thickness d*. The formulation can be derived, using the results of Section 4.4, as follows:

Д Oi=^{qb*) (9.48)

ds

where q is the local streamwise velocity component of the potential flow (outside the boundary layer) and the differentiation takes place along a streamline s. The transpiration velocity then becomes qn. = Да,. For more details on this approach see Ref. 9.2.