Additional constraints
Any number of other constraints can be added in addition to the lift, such as the root bending moment mentioned earlier. An effective general solution technique here is define a Lagrangian function L, which is the objective function plus all the constraints,
L(a^(s) , Л1 , Л2 …) = Di + Л1 (L — Lspec) + Л2(М0 — M0spec) + … (5.102)
where the Лі,2… coefficients are Lagrange multipliers associated with the constraints, and are solved as part of the problem. The constant Л in the previous section was in fact the same as Л1 here.
The constrained-optimum solution Ap(s), Л1, Л2 is defined by the requirement that L is stationary.
5C = 5Di + 5Лі (L-LSpec) + ^2 (Mo-Mospec) + Лі 5L + Л2 SMo = 0 (5.103)
|
P* A Sp |
|
y cos в + z sin в P^V* Ap cos в ds – Lspec |
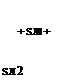 |
Substituting for 5Di, SL, 5M0, L, M0, and collecting terms having the same A Sp, 5Л1,5Л2 factors gives
|
N У Aij Apj – Л1 V* cos ві j=1 |
|
P*V*y A pi cos ві Asi |
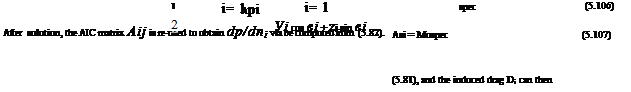 |
which for optimality must be zero for any A6p(s), dA , dA2. This requirement is met by setting all the quantities in the brackets to zero, using the wake panel method to discretize the integrals. Since the first bracket is inside the integral (and inside the equivalent discrete sum), it must be set to zero at each of the N discrete panel points. In contrast, the second and third brackets set to zero are single equations. The result is the following (N+2) x (N+2) linear system for A pi, Л1, Л2.











