Axis Systems

In computational methods, the aircraft motion vectors U, О, and the aerodynamic force and moment vectors F, M are most easily specified or calculated in the same xyz axes which are used to specify the geometry itself, shown in Figure 6.1. To apply the results to aircraft performance, stability and control, and other related disciplines it is necessary to provide these vector quantities in other more relevant axes.

6.2.1 Stability axes

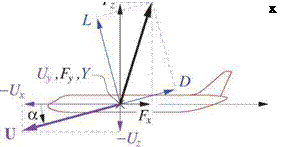
The drag, sideforce, and lift force components are most commonly defined in the stability axes, which are rotated from the geometry axes by only the angle of attack a (not by sideslip в), as shown in Figure 6.2.

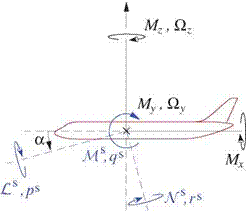
Figure 6.2: Orientation of stability-axis (freestream-aligned) aerodynamic force components D, Y,L, moment components Ls, Ms, Ns, and rotation rate components ps, qs, rs.

All the standard vector components in stability axes are defined from their components in geometry axes using the T rotation matrix.

(6.4)

Note that the moment and rotation-rate components, Ls, Ns and ps, rs, have reverse signs compared to the force components D, L. In effect, the stability axes used for the moments and rates are rotated by 180° about the y axis relative to the stability axes used for the forces. Note also that the T matrix leaves all the vector y components unchanged. Hence we have Y = Fy, Ms = My, qs = Qy.

6.2.2 Wind axes

The stability axes are not quite appropriate when examining the drag of an aircraft in sideslipping flight with

/1/0, since the drag I) as defined by the T matrix in (6.5) is not the hue stream wise drag force. In this

= W

situation we can invoke the wind axes, which are implemented by the rotation matrix T, which consists of a and в rotations, applied in that order as shown in Figure 6.1.

w

w

Note that the drag as defined by the T matrix in (6.6) is exactly equivalent to the dot product of the total force and the unit freestream.

D = F ■ V//!/ (6.8)

= W = s

Furthermore, the sideforce Y produced by T in (6.6) is almost the same as that produced by T in (6.5), and the lift L is identical. Because the simple relation (6.8) is available to define the exact D when needed, and the exact Y is of relatively little importance, wind axes see little use in practice.