Beddoes’s Generalized Wake Model

Another parsimonious but very effective prescribed wake model has been devel­oped by Beddoes (1985). In this model, it is also recognized that axial (vertical) trajectories of the tip vortices can be estimated if an assumption for the inflow distribution across the disk is made. Beddoes suggests the model

D = A.0 (l + Ex’ – E (y)3 l) , (Ю.81)

where x’ — x/R and у’ = y/R, deducing this form of the inflow from the measurements of Heyson & Katzolf (1957). Again, the evaluation of A., is based on momentum considerations. Beddoes suggests that E = x, where x is the wake skew angle, although this is generally too large and E = x /2 has been found to give better agreement with experimental results and with the FVM.

Although with these assumptions the solution for the wake can be obtained by solving directly Eq. 10.53, this still involves significant expense because of the repeated evaluation of the Biot-Savart law. Instead, Beddoes (1985) specifies the equations describing the wake. At the rear of the disk, in the region occupied by the wake,

V = 2Л.0 (l – E (y[/f |) , (10.82)

so that the vertical displacement of the tip vortex is given by

zip = – B’lfw + / bdfb, (10.83)

Jo

where z’ = z/R. Now, if л:’ір < — cos(t/q> — ^w) then the element on the vortex filament has not convected beyond the rotor disk and

Ґ" kdfb = – V) (l + E(cos(fb – + 0.5!Xtyw – I0>t’,p)3|)) *»• (10-84>

If cos(V^ — fw) > 0 then the vortex element has always been downstream of the rotor disk and in this case

If neither of the preceding conditions are met, then the element has spent part of the time within the disk and the remainder downstream of the disk and for this condition

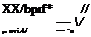
(10.86)

РЛС / ( О P (Лп Kocic nf fll ас Д o/~l lirjfi /л n г tb л rvf

wu CK^pp/ ywu/v). UU HRS Odolo v)l ulCoC СЦиаииію, ui^ lihv^ wumpuu^iao ui

the tip vortex location with respect to the rotor can be calculated.

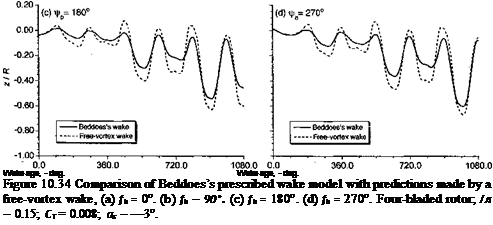Figure 10.34 shows a comparison of the vertical components of the tip vortices in forward flight at д = 0.15 as obtained from the Beddoes prescribed-wake model and also from a FVM. Because the differences between the prescribed wake and the free-vortex wake are now much smaller compared to the rigid wake, for clarity the results in Fig. 10.34 are plotted in terms of vertical displacement versus wake age relative to the blade of origination. The agreement is good, and bearing in mind the relative simplicity of the prescribed-wake solution compared to the free-vortex wake (at least two orders of magnitude less expensive to compute), it is certainly a modeling option to consider in any form of rotor analysis. After the wake geometry is known, the induced velocity field can be computed through the application of the Biot-Savart law to the discretized vortex filaments. Because this incurs the highest cost of any vortex wake model, Beddoes (1985) suggests an alternative and

highly simplified approach of approximating the induced velocities from some elements of the wake by using elongated straight line segments, which retains the simplicity and low cost of semi-analytic models such as when using vortex rings.

Beddoes’s prescribed wake model seems to have received good attention from rotor analysts, and has been used in a number of aerodynamics and acoustic studies, mainly because of its excellent computational efficiency. Van der Wall (2000a) has performed an evaluation of the Beddoes wake model against measured airloads, wake displacements and В VI locations over the rotor disk in forward flight and has also suggested further improvements to the model – see van der Wall (2000b). While the predicted results seem good, it must be remembered that the tip vortex trajectories are still being prescribed a priori based on some generalized assumptions and not calculated based on the actual induced flow velocities near the rotor. Therefore, in the strictest sense, the prescribed wake model must be viewed as a postdictive model and must be validated for each and every rotor configuration, which is a formidable undertaking. The main problem, however, is this type of wake model does not offer the analyst much flexibility in terms of rotor design, despite the modest computational cost. This sought-after flexibility is obtained only with the next level in wake modeling, which is called the free-vortex wake method (FVM).