Constant-Strength Doublet Distribution

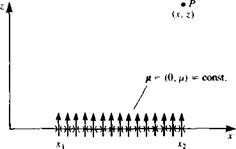
Consider a doublet distribution along the x axis consisting of elements pointing in the z direction [ц = (0, /і)], as shown in Fig. 10.7. The influence at a point P(x, z) is an integral of the influences of the point elements between x,-*x2:

and the velocity components are «(*> z) = ^f 7C Jr

-X. [(*-*o)2 + 22]2 Note that the integral for the w component of the source distribution is similar to the potential integral of the doublet. Therefore, the potential at P (by using Eq. (10.21)) is

FIGURE 10.7 Constant-strength along the x axis.
doublet	distribution
(10.26)
(10.27)
(10.28)
Comparing this expression to the potential of a point vortex (Eq. (10.8)) indicates that this constant doublet distribution is equivalent to two point vortices with opposite sign at the panel edges such that Г = fi (see Fig. 10.8). Consequently, the velocity components are readily available by using Eqs. (10.9) and (10.10): u=±———- ?] (Ю.29)
(10.30)
FIGURE 10.8 Equivalence between a constant-strength doublet panel and two point vortices at the edge of the panel.

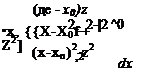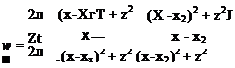When the point P is on the element (z = 0±, хг<х <x2) then following Section 3.14

Ф(х, 0±) = T^

and the velocity components become

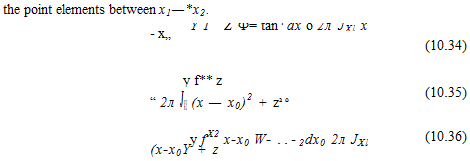and the w velocity component is singular at the panel edges.

Details of the integral for the velocity potential appear in Appendix В (Eq. (B.10)) and in terms of the distances and angles of Eqs. (10.15) and

FIGURE 10.9

Constant strength vortex distribution along the x axis.

(10.16) (as shown in Fig. 10.6) it becomes

Ф=~2ж [^_ДСі)01_^_д:2^2 + ^1п^] (10.37)

and in terms of the x-z coordinates:

^ У Г, . Z. . _. z z, (x-x^f + z2!

Ф = ~2л l * _ tan 7=^-(Ar""2)tan ^ + 2,n0c-x2)2 + z2J

(10.38)

Following the formulation used for the constant source element, and observing that the и and w velocity components for the vortex distribution are the same as the corresponding w and u components of the source distribution, these equations become

tan 1 tan 1 X—X2 X— JCjJ	(10.39)
Г (x-x2)2 + z2 4л {x – хг)2 + z2	(10.40)

The influence of the element on itself at z = 0± and (д:г <x <x2) can be found by approaching from above the x axis. In this case вг = 0, в2 = я and

Ф(*> 0+) = К* – *i)0 — (де — х2)я] – % (x – x2) (10.41a)

Similarly, when the element is approached from below, then

Ф(х,0-) = -^(х-х2) (10.416)

The x component of the velocity can be found by observing Eq. (10.24) for the source or by recalling Section 3.14,

n(x,0±) = ±^ (10.42)

and the w velocity component is similar to the и component of the source (Eq.

(10.23) ):

K4*;0±)=£lnji^ (10.43)

In most situations the influence is sought at the center of the element where rx = r2 and consequently w(panel – center, 0±) = 0.