Decay of a Potential Vortex

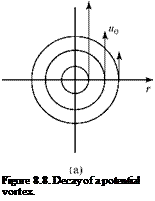
Consider a two-dimensional potential vortex at the origin of coordinates in an incom­pressible flow, as shown in Fig. 8.8a and discussed in Chapter 4. The fluid is inviscid and the velocity field is given by V = Г/2пг, where Г is the strength of the vortex.

The potential vortex continues the behavior shown in Fig. 8.8a indefinitely in the absence of viscosity. Now, imagine that at a time t = 0, a viscosity switch is turned on so that the fluid instantaneously becomes viscous, whereas nothing is done to sustain the strength of the potential vortex. A prediction of the resulting flow field requires the solution of a linear, time-dependent form of the Navier-Stokes equations.

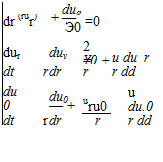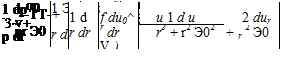The continuity and momentum (Navier-Stokes) equations in polar coordinates become:

The student should verify these equations. (Examine the equation following Eq. 3.54 and Example 3.10 but recall that both the time dependence and the viscous stresses must be retained in the present situation.) Notice that the momentum balance was divided through by the (constant) density so that the kinematic viscosity appears in the viscous terms. For the conditions specified, it is assumed that streamlines are circular (as they are in the potential vortex); thus, the radial velocity component, ur, is everywhere zero. The continuity equation reveals that the circumferential velo­city, u0, cannot be a function of 0 and therefore is a function only of time and radial

position. It also is apparent that none of the variables can depend on the angular position by symmetry. The 0-momentum equation then reduces to:

The solution of this linear equation is found by standard methods (see Exercise 8.26) to be:

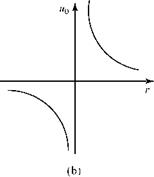
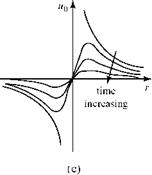
U0(r>[1 “e(f2/4vt)] (8-25)

and is shown with solid lines in Fig. 8.8c for increasing values of time. The constant of integration is expressed in the form of the vorticity, Г, for a potential vortex. Notice that when viscosity is introduced into the flow model, the infinity in flow velocity at the origin (i. e., a physical impossibility) disappears. At the origin, the viscous vortical flow exhibits solid-body rotation. As time progresses, the vortex decays and, ulti­mately, the signature of the vortex in the flow field disappears. This is the observed behavior of the vortices trailing behind the wings of an aircraft, and the disturbance eventually is smeared out by the action of viscosity. The kinetic energy originally contained in the potential vortex is dissipated by viscosity and changed into internal (i. e., thermal) energy, resulting in a (slight) increase in air temperature. In addition to being of interest because it represents an exact solution to the Navier-Stokes equations, the solution for a decaying vortex (sometimes called a Taylor, or a Lamb, vortex) is useful as an exact benchmark solution against which to validate certain CFD codes.

Notice that it was not necessary to use the radial-momentum equation to find the velocity solution. However, the radial momentum yields additional information of interest; namely, the pressure distribution through the vortex as a function of time. The r-momentum equation reduces to:

2 л

p ul = 2E, (8.26)

v r dr’

which can be integrated to yield the pressure from the known solution for the velo­city, u0. The result (refer to Exercise 8.26) shows that the pressure has minimum value at the center of the vortex (zero pressure in a potential vortex). Hence, a par­ticle trapped in the center of a vortex tends to stay there until it can overcome the radial pressure gradient.