Derivation of the Boundary-Layer Equations

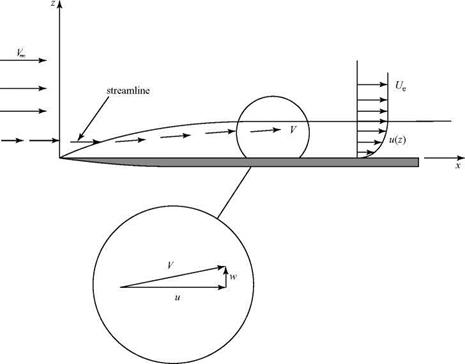
Consider a thin flat plate extending to downstream infinity and aligned with a steady, incompressible flow, as shown in Fig. 8.10. The characteristic length L introduced pre­viously now represents a fixed distance downstream of the plate leading edge. The flat plate is the simplest possible geometry. This simplifies the initial discussion of the boundary layer because no streamwise pressure gradients require attention. Later, we present the effects of pressure gradients that are introduced by the presence of the body in the flow or by an externally impressed pressure variation. The velocity at the edge of the boundary layer is essentially that of the oncoming freestream, V<». In what follows, the symbol Ue is used to represent the edge velocity instead of Vж and the pressure-gradient terms are retained in the defining equations. This allows for subsequent generalization to flows with local streamwise pressure gradients and, consequently, with Ue = Ue(x) rather than Ue = V^ = constant.

At the surface of the plate, the velocity is zero (no-slip). At the edge of the thin boundary layer the velocity is Ue. The velocity rapidly increases from zero to Ue within a very short distance, so that within the boundary layer the vis­cous shear stress (p 5u/5z) must be very large. This region of significant shear stress defines the boundary layer thickness, 5(x), which varies along the surface as suggested in Figure 8.10. Outside of this region of nonuniformity the velo­city gradients are small and the shear stress is negligible, so that the region may be taken to be potential flow field (frictionless). Experiments confirm that not only is 5 << x but also db/dx << 1. That is, the boundary layer thickness increases slowly so that within the boundary layer the velocity normal to the surface is very small compared to the streamwise value, that is, w << u, as shown in Fig. 8.10. The bound ary layer thickness, 5, increases continuously with x because the stream – wise momentum of the flow particles located further and further away from the surface is being reduced by the continuing shear force at the surface. Since the boundary layer thickness increases with distance downstream, continuity requires that the mass flow within the boundary layer must also be increasing. This means that streamlines pass into the boundary layer from the freestream flow as sug­gested in Fig. 8.10.

Equations (8.29) govern the flow described in Figure 8.10. However, this is a set of nonlinear partial differential equations in spite of the simplifications intro­duced already. There are no general solutions to this set. Clearly, one must either find additional valid simplifications or resort to a strictly numerical approach. The latter technique (CFD) is now in vogue due to the ready availablity of high-speed computers. However, valuable physical insight is lost if we yield to this “easy way out” at this juncture.

We proceed now to simplify the Navier-Stokes equations to the boundary layer equations, which are valid for 5/x << 1 and Re >> 1. This will be done by first esti­mating the size of each term in the nondimensional Navier-Stokes equations and then dropping some terms as being negligibly small compared to those retained. The same approach will be used later in deriving linearized compressible flow theory, although here the development will be a bit more formal. The opportunity is taken at this point to familiarize the student with the modern analytical methods that have been developed to handle the type of mathematical problem arising in the boundary layer situation. These methods, now often referred to as singular per­turbation techniques, apply to a wide variety of similar problems and yield a vital physical insight.

Because it is necessary in the following discussion to compare nonambigu­ously the sizes of various quantities, it is useful to introduce a special notation to accomplish this. We work here with properly nondimensionalized quan­tities, as introduced in Section 8.5. The thickness of the boundary layer is a convenient length scale to use within the boundary layer because there is no natural length scale available in the boundary-layer problem. (In most cases, the physical length of the body is essentially infinite compared to the thickness of the boundary layer.) The chord length of an airfoil, or the length of the flat plate in a flow experiment, is too large to represent a useful measure of the properties of the thin fluid layer near the surface in which rapid changes in velocity take place.