Flow Rotation Effects on Turbulence Inside Vortices

The forgoing analysis presents a somewhat oversimplified model of the charac­teristics of blade tip vortices, although these models are still found to give good average approximations to their behavior. When taken to a deeper level, however, the structure of the tip vortices is known to have regions of both laminar and turbulent flow separated by a re­gion of transitional flow. Such concepts of the vortex structure stem from early experimental observations made by Hoffman & Joubert (1963) and Tung et al. (1983).

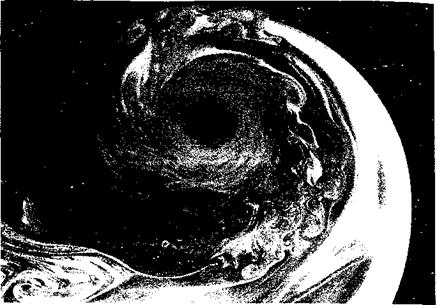
For example, flow visualization performed on a tip vortex emanating from a rotating blade is shown in Fig. 10.24. It can be seen that the flow is predominantly laminar near the core region, which is marked by a region of smooth flow where there are no interactions between adjacent fluid layers. This is followed by a transitional region that has eddies of different sizes. Outside of this there is a more highly turbulent region – see also Fig. 10.4. This multi-region vortex structure concept differs from the descriptions assumed by the previously mentioned mathematical models in that it is neither completely laminar like

the Lamb-Oseen model nor completely turbulent like Squire’s or Iversen’s model. Recent high-resolution velocity measurements made using LDV [see Martin et al. (2001), Martin & Leishman (2002), and Ramasamy & Leishman (2003)] also continue to support the idea of a multi-region laminar and turbulent structure of the tip vortex.

The extent of these three regions of the vortex are affected by the vortex Reynolds number, Rev. In particular, the effects of flow rotation on the development of turbulence present inside the vortex has been hypothesized to play an important role in determining the structure of a vortex – see Hoffman & Joubert (1963), Cotel & Breidenthal (1999), and Holzapfel et al. (2001). Rayleigh’s centrifugal instability theory [see Rayleigh (1880)], which uses a buoyancy force concept, suggests that the vortex will never develop turbulence provided that the product of velocity and radial distance increases with the increase in radial coordinate. Only a few vortex models [e. g., Donaldson (1971) and Baldwin et al. (1973)] have been developed that recognize this concept. However, the various properties of the vortex flow predicted using these models, such as the core growth and the velocity profiles, did not correlate well with experimental results available at that time.

Bradshaw (1983) developed an analogy between rotating flows and stratified fluids. His analysis is based on the theory that flow rotation causes the higher speed fluid to prefer the outside of the vortex while conserving angular momentum, even if the density is assumed constant throughout the vortex. Using energy principles, an expression was developed for the local strength of the analogous stratification expressed as an equivalent gradient Richardson number, Ri. This number comes directly from the turbulent kinetic energy budget equation [see Bradshaw (1983) and Holzapfel et al. (2001)] and is basically a ratio of the turbulence produced or consumed inside the vortex as a result of buoyancy (centrifugal effects) to the turbulence produced by shearing in the flow. It can also be thought of as the ratio of potential to kinetic energy in a stratified flow.

Bradshaw’s Richardson number involves the evaluation of the swirl velocity gradients in the vortex flow. Holzapfel et al. (2001) corrected Bradshaw’s original definition, for which the revised expression is given by

Cotel & Breidenthal (1999) and Cotel (2002) used this stratification concept and have de­termined a threshold value for the Richardson number that is a function of vortex Reynolds number. This analysis is based on a nondimensional parameter called a “persistence pa­rameter,” which is defined as the ratio of rotational to translational (convection) speed of the vortex. If the persistence parameter is high, which is the case for most helicopter rotor wakes, the threshold value of the Richardson number was determined experimentally to be ReT. This means that the tip vortex will be laminar up to a radial distance where the local gradient Richardson number falls below this threshold value. Any turbulence present inside this boundary will be either relaminarized or suppressed; even substantial eddies will not be able to penetrate this vortex boundary.

The local gradient Richardson number has been calculated using the measurements from Ramasamy & Leishman (2003) and is shown in Fig. 10.25, along with the Lamb-Oseen and Iversen vortex models. The local Richardson number variation for both the vortex models (and the measurements) is seen to approach infinity at the center of the vortex. As the radial distance from the center of the vortex increases, the Richardson number quickly reduces in value and falls below the assumed stratification threshold (i. e., for values of Ri above the stratification threshold only laminar flow is possible). In this region, diffusion at a molecular level will be the only means to transport the momentum contained in the vortex flow.

This concept helps explain the persistence of lift generated tip vortices, in general, to relatively old wake ages. When Ri is below the stratification threshold, flow turbulence can develop. This argument serves to augment the hypothesis of a multi-region vortex where

the flow is always laminar well inside the core region, the flow which then progressively transitions to turbulence through and outside the tip vortex core. This mechanism certainly affects the induced velocity field, especially closer to its axis, and the effects of flow turbu­lence must be considered carefully if higher fidelity vortex models are to be developed for helicopter rotor applications. Such models must delineate the effects of vortex Reynolds number so that the models can be applied to a wide range of rotor scales and operating conditions.