Implementation of Radiation and Outflow Boundary Conditions

The optimized central difference scheme for approximating spatial derivatives introduced in Chapter 2 will give rise to ghost points (points outside the compu­tational domain) at the boundaries of the computational domain. For a 7-point stencil, 3 ghost points are created. To advance the entire computation to the next time level, a way to calculate the unknowns at the ghost points must be speci­fied. Here, it is suggested that this is done using the radiation or outflow boundary conditions.

Figure 6.1 shows the upper right-hand corner of a computation domain. Three columns or rows of ghost points are added to form a boundary region surrounding the original computation domain. For grid points inside and on the boundary of the interior region, Eqs. (5.28) and (5.29) discretized according to the DRP scheme are used to advance the calculation of the unknowns to the next time level. In the bound­ary region it will be assumed that the solution is made up of outgoing disturbances satisfying the radiation or outflow boundary conditions of Eq. (6.2) or Eq. (6.13). The time derivatives of these equations are discretized in the same manner as described in Chapter 3. These equations are to be used to advance the solution in time. Now, all the variables in the boundary region as well as in the interior regions can be advanced in time simultaneously. To approximate spatial derivatives, symmetric spatial stencils are not always possible for points in the boundary region. The opti­mized backward difference stencils of Chapter 2 are to be used whenever necessary. An example of such backward difference stencils is illustrated by that of the corner point B in Figure 6.1. In the boundary region, the domain of dependence of the outgoing waves is consistent with that of the backward difference approximations.

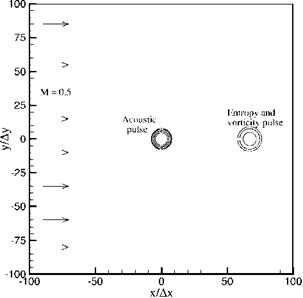
Figure 6.2. Computational plane show­ing a uniform mean flow of Mach 0.5 and initial acoustic, vorticity, and entropy disturbances.

Unlike the use of unsymmetric stencils at interior points where waves may propagate in any direction, no numerical instability would be created unless there are strong reflections of waves back into the interior.